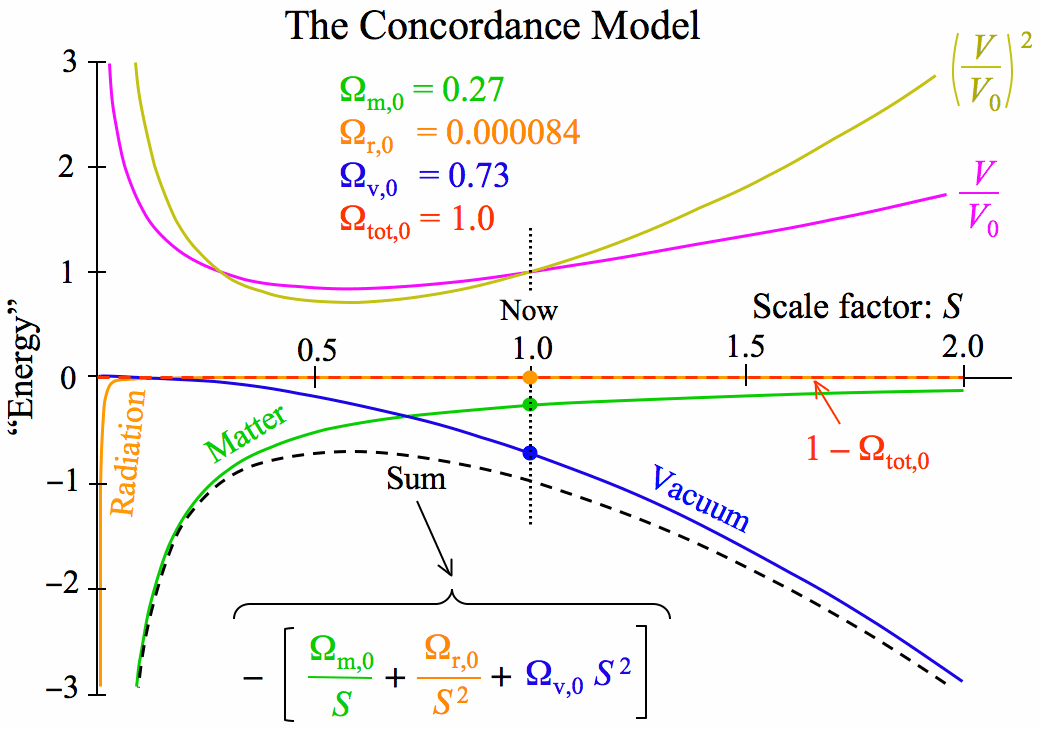
"Energy" Curves for the Concordance Model

Energy curves for the Freidmann concordance model. The gravitational PE terms are plotted negative and sum to make the dashed "hilltop" curve. The Friedmann equation demands that the velocity (squared) curve is the mirror symmetry of this about the total energy term (1 - _t,o) which is zero for the concordance model. Taking the square root of the (v/v_o)² curve gives us the velocity itself, v(a)/v_o. The current Omegas are shown as filled dots at a = 1.

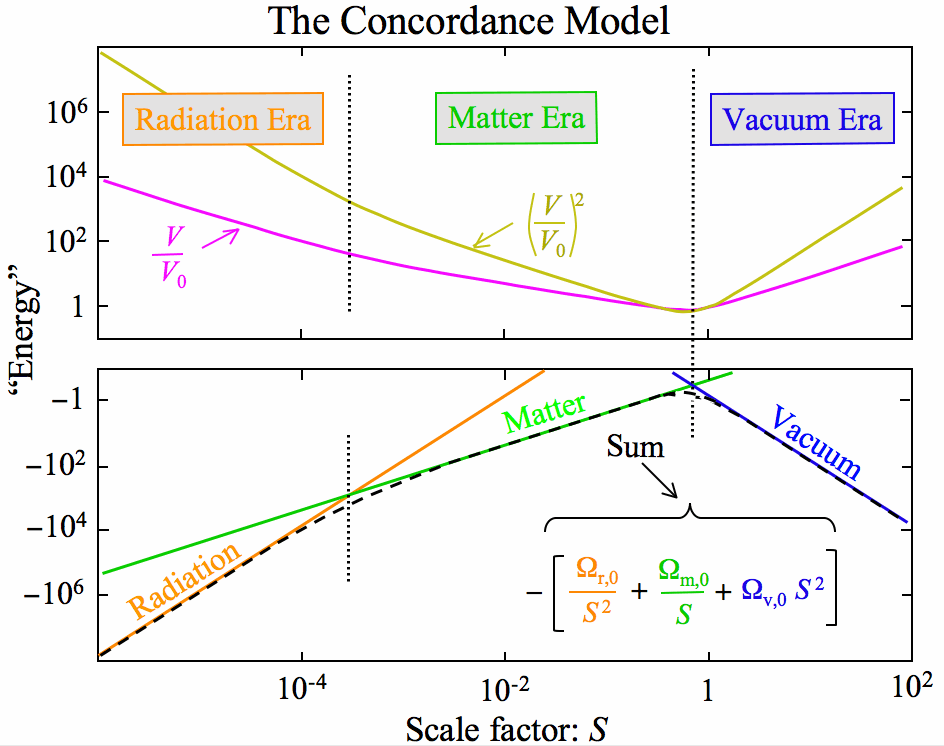
The same relation is plotted but with logarithmic axes. All power laws turn into straight lines: in the radiation era v(a) a^-1, in the matter era v(a) a^-½, and in the dark energy era v(a) a.

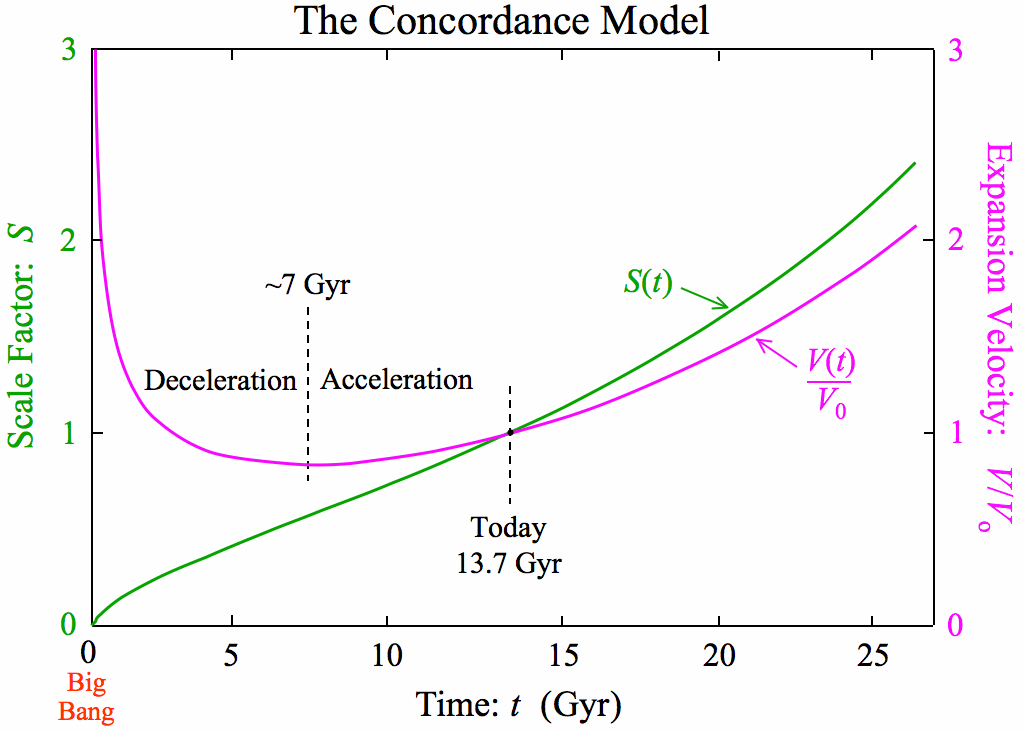
The function v(a) has been converted to v(t) and a(t), which are plotted using linear axes. Obviously, v(t) is given by the gradient on a(t). Notice that the change from deceleration to acceleration, which occurs when the total gravitational term has is peak, is before the time of equal matter and vacuum densities (where the green and purple lines cross in the top figure).

Figure: Whittle's (upcoming) undergraduate text.