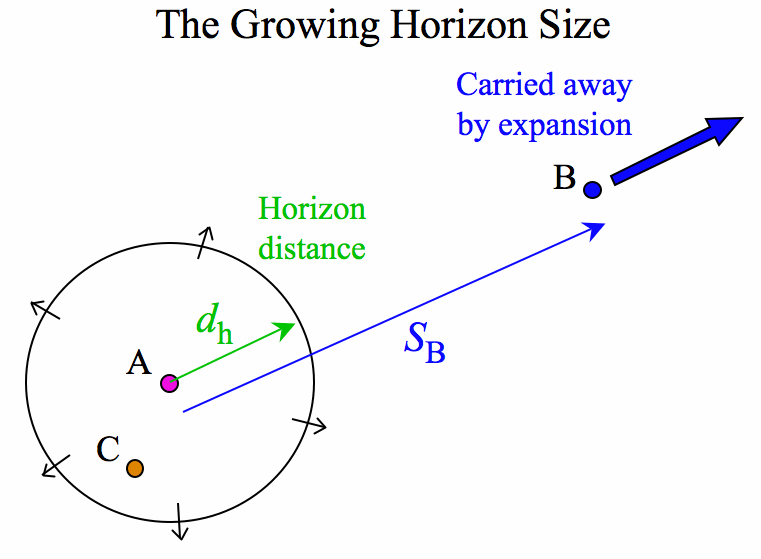
At some time after the Big Bang, A has a horizon around it. At this time, region C is inside the horizon while region B is outside. When did/will C/B enter the horizon? Are there any locations that are inside the horizon at arbitrary early times?
Here's a graph of the growth in the separation of C and B from A (a 
t1/2 in the radiation era), and the growth of the horizon (dh t). The times at which C and B enter the horizon are clear enough. However, all lines superficially appear to cross at the origin -- was everything "in contact" at the instant of the Big Bang? No -- to see this simply replot the axes in exponential form.
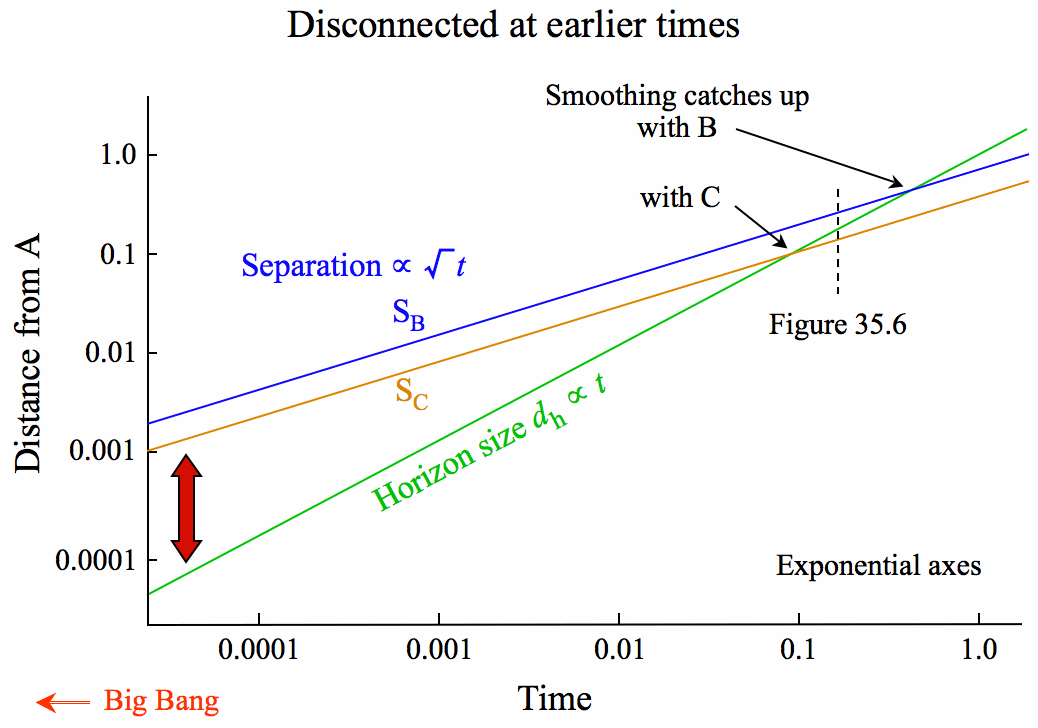
Clearly, at earlier and earlier times, less and less material is inside A's horizon. The fundamental reason is that the slope of the horizon line is steeper than the slopes of the expansion lines. Since these slopes give velocities, and since the horizon grows at constant speed, then the horizon problem always exists for decelerating expansion. Conversely, if the expansion is accelerating (e.g. a tn with n > 1, so v tn-1), the situation is reversed, and all regions are inside the horizon at earlier and earlier times.
Figures from Whittle's Teaching Company Course, and upcoming undergraduate text.