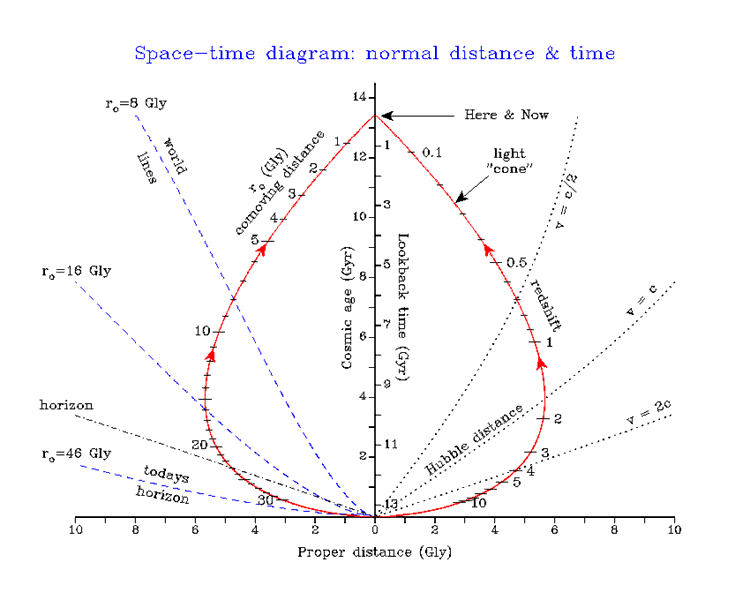
Light cone diagram using proper distance and normal time.
Solid red line shows, on both sides, the trajectory of a light ray which starts at the big bang from our current particle horizon. It is also the event-line which we witness now as light comes to us, ie we see only those events lying on the red line (light rays starting at other space-time events have either already arrived or will arrive in the future) -- the light cone is for light arriving now. Notice that for the first 4 Gyr, the light is actually getting further from us, carried by cosmic expansion. At 4 Gly it crosses the Hubble distance at that time (ie expanding at c) and finally begins to get closer. Other lines of constant expansion speed are also shown (c/2 and 2c). Notice that the light cone finally arrives at 45 degrees, since locally the expansion is essentially zero.
Redshift, z, and comoving (current) distance, ro, scales are also indicated on the right and left halves of the light cone (note that the ro values match the world line values at their intersection).
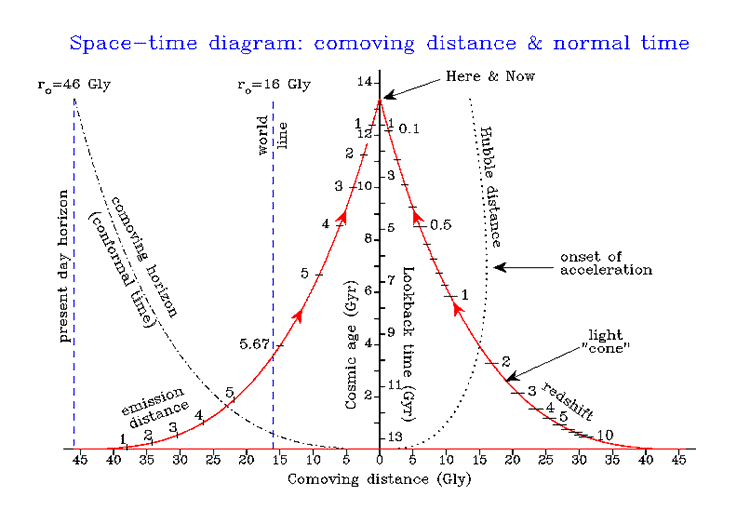
Light cone diagram using comoving distance and normal time.
As before, the black dot-dashed line shows the expanding particle horizon, meeting
the 46 Gly world line of our current particle horizon at time t=now. This distance,
in comoving coordinates, is also equal to c  conformal time, which
will be used as the time axis in the third and final space-time diagram.
conformal time, which
will be used as the time axis in the third and final space-time diagram.
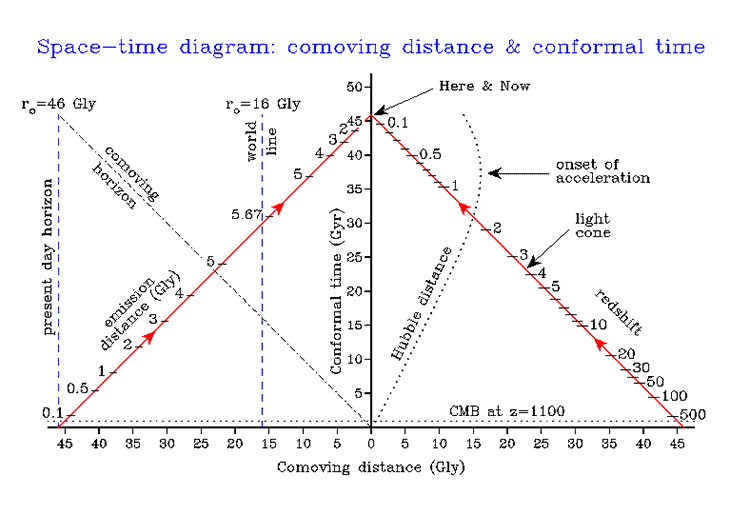
Line cone diagram using comoving distance and conformal time.
 (t) =
(t) =
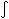 dt/a 0 to t), and plot these at the same scale.
As before, redshift and emission distance are marked along the cone. Notice how
rapid early expansion stretches conformal time near the big bang, so
that even the CMB is visibly offset from the y=0 axis (and would be impossible to
see with a normal time axis).
dt/a 0 to t), and plot these at the same scale.
As before, redshift and emission distance are marked along the cone. Notice how
rapid early expansion stretches conformal time near the big bang, so
that even the CMB is visibly offset from the y=0 axis (and would be impossible to
see with a normal time axis).
Notice that the Hubble distance is rapidly decreasing during acceleration, and in fact becomes zero at conformal time 65 Gly, which corresponds to the infinite future (we see a smaller and smaller comoving part of the Universe as exponential expansion proceeds).
Figures made for this website.