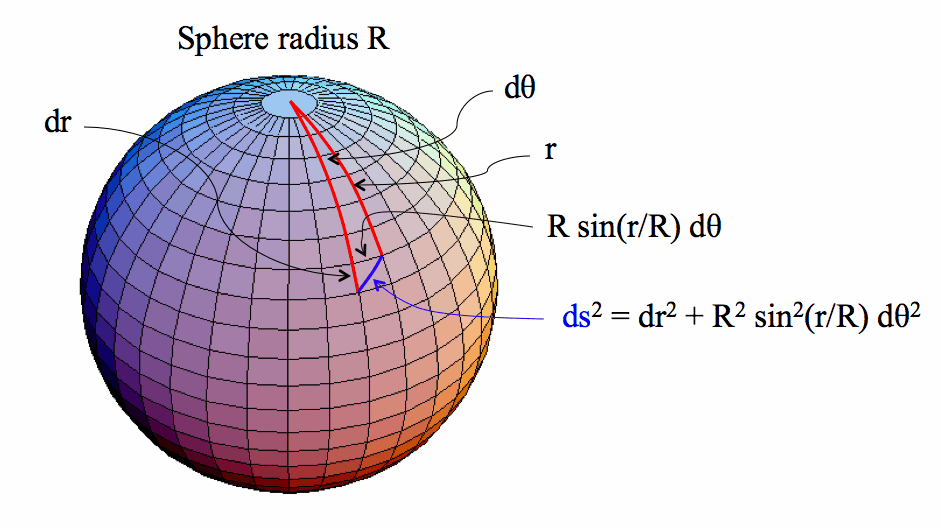
The length of the small blue arc is given by the Pythagorean (i.e. locally flat) right triangle, with sides dr and R sin(r/R) d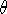
. Notice that r/R is the angle (in radians) subtended by r at the center of the sphere. Clearly, the blue arc is smaller than it would be if the red lines were drawn on a flat piece of paper, for which the sides would be dr and rd (without the pre-factor R sin(r/R) ).
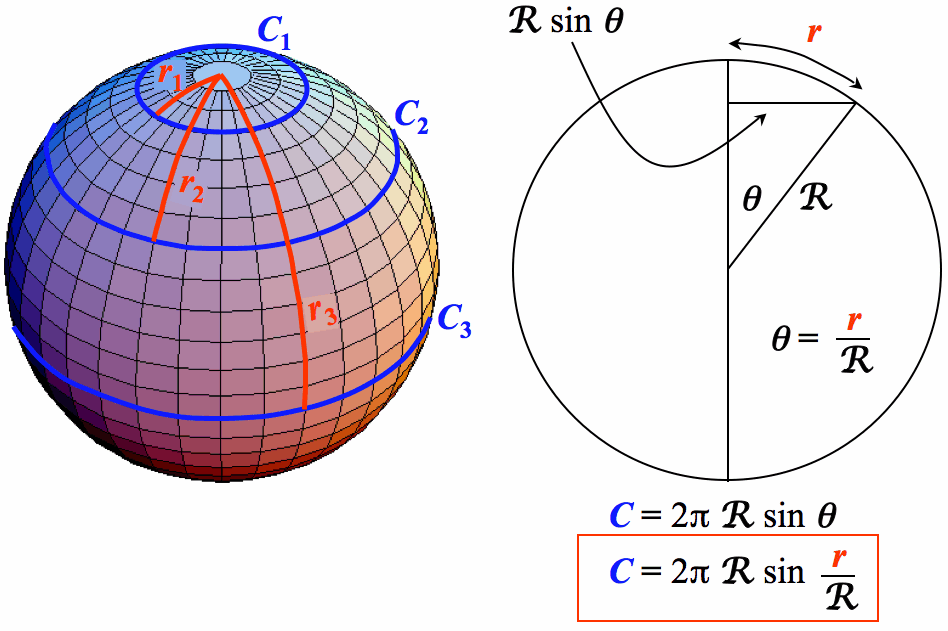
Integrating the line element ds around a circle of constant radius r gives us the circumference relation: C = 2 
R sin(r/R).
Figure: Whittle's (upcoming) textbook.