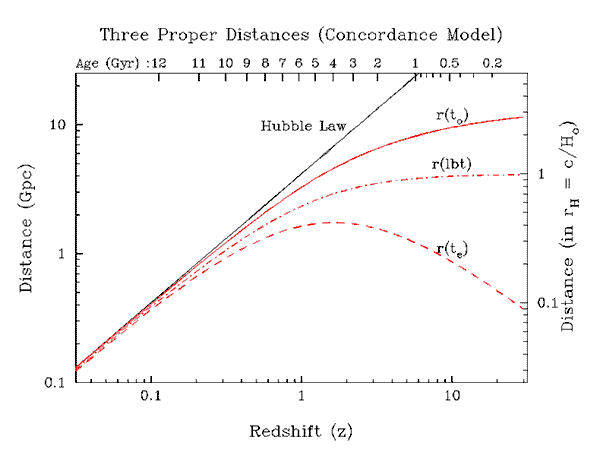
Principle distances for the concordance model
Current distance: r(to); Emission distance: r(te); light travel distance: r(lbt)
The linear Hubble law is also shown for comparison.
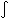 -dz / E(z) (z to 0);
The distance when the light set out is the smallest, r(te) = r(to / (1+z); and the distance light itself travelled is intermediate: r(lbt) = rH,o
-dz / E(z) (z to 0);
The distance when the light set out is the smallest, r(te) = r(to / (1+z); and the distance light itself travelled is intermediate: r(lbt) = rH,o 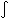 -dz / (1+z)E(z) (z to 0). This latter distance is the one
most often used in "popular" discussion, since it is linked to the look-back-time. The
distance at emission famously passes through a maximum at z
-dz / (1+z)E(z) (z to 0). This latter distance is the one
most often used in "popular" discussion, since it is linked to the look-back-time. The
distance at emission famously passes through a maximum at z  1 since long ago the Universe was smaller and everything was closer. This is the distance that is used to evaluate angular diameters, which is why objects appear larger at high redshift -- they were in fact much closer when their light set out.
1 since long ago the Universe was smaller and everything was closer. This is the distance that is used to evaluate angular diameters, which is why objects appear larger at high redshift -- they were in fact much closer when their light set out.
The age, t(z), is given at the top, and the distances are given relative to the Hubble distance, rH,o = c/Ho = 13.88 Gly on the right
Figure made for this website.