The Evolving Power Spectrum

These figures show how the initial power spectrum, P(k) ~ k1, is changed into a gently peaked form, preserving the initial slope on large scales but introducing a steeply falling spectrum P(k) ~ k-3 on smaller scales.

The following figures were made using a rough model:

  • Hubble radius, rH, is set to ct at all times (rather than 2ct and 3ct/2 in the radiation and matter eras).
  • We simply set k = 1/ (instead of 2/) with all lengths in Mly.
  • Simple dynamics: a ~ t½ and t2/3 in the radiation and matter eras, with a sudden change at teq = 0.057 Myr; zeq = 3700.
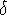
  • The slow growth of / during the radiation era is initially set to zero (refined model modifies this).
  • No other influences (early or late) on P(k) are included !
     
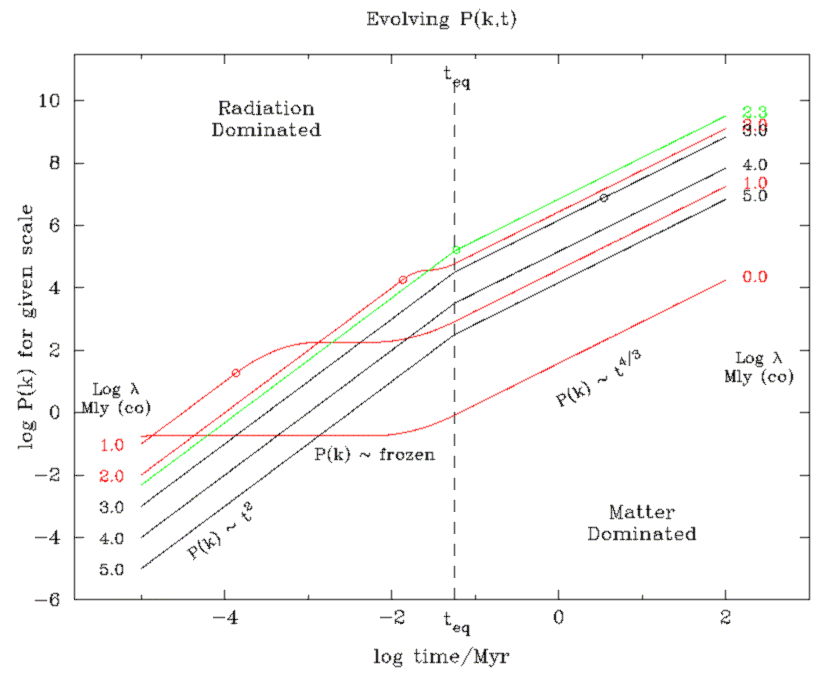
First Figure shows growth of Hubble sphere (blue line; gradient unity); along with the growth in proper size of any perturbation following cosmic expansion (i.e a t½ up to matter-radiation equality, and t2/3 thereafter). The evolving sizes of four lengthscales are shown, corresponding to current (comoving) sizes of 10 Mly, 100 Mly, 220 Mly, and 2200 Mly. Notice the first two cross the Hubble sphere during the radiation era (red lines); while the latter two cross it in the matter era (black & green) -- with 220 Mly marking the boundary (green). Note also that wavelengths differing by 1 dex now, crossed the Hubble sphere at times differing by two dex in the radiation era (because the Hubble radius grows linearly with time, but the wavelengths grow as t½).

Perturbation growth factors for / are also labelled.
Recall that P(k) ~ (/)2 so growth in P(k) is "double" that of /.

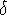
There are four cases to consider (see below the figure):

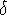
  1. Super-Horizon Radiation:   /     a2     t. This is just the differential expansion rate of slightly over/under dense regions (ie slightly closed/open mini-universes).
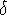
  2. Sub-Horizon Radiation:   / is essentially frozen. The density is dominated by radiation which is trapped by the baryons and oscillates. Dark matter's self-gravity is dwarfed by the radiation and so its perturbations can't grow. In truth, growth continues for a while after horizon entry until the initial velocity is redshifted away; and the CDM can grow logarithmically during this period. In this toy model, we set the growth in this period to zero.
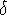
  3. Super-Horizon Matter:   /     a     t2/3. This is identical to the super-horizon radiation growth, except the gentler deceleration in the matter era (since ~ a-3 rather than a-4) slows the growth rate by one power of a.
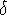
  4. Sub-Horizon Matter:   /     a     t2/3. This is a famous result, because expansion slows collapse of overdensities compared to a static universe. Notice that this growth rate is the same before and after horizon entry -- so there is no change associated with horizon entry.

The key point is that while the primordial spectrum, P(k)     k, suggests that smaller wavelengths should have stronger perturbatons, we notice that it is the smaller wavelengths that enter the horizon much sooner and so are prevented from growing relative to larger wavelengths which enter later. Quantitatively, consider the two red curves with comoving size 100 Mly and 10 Mly. Their scales differ by 1 dex, so Pinit(k) is 1 dex higher for the 10 Mly scale. But this enters the horizon two dex earlier. During those two dex, the 100 Mly scale continues to grow by two dex in 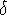/ before it too is frozen. Both remain frozen until they are released at equality and from then on they each experience the same growth. During that 2 dex delay, P(k) for the larger wavelength grew by a huge 4 dex ! Thus, when we consider the spectral index between the two wavelengths after equality, it has changed by 4, going from P(k)   k1 to P(k)   k-3.

This only works when modes enter the horizon during the radiation era. The biggest scale that does this is 220 Mly (in this toy model), shown in green. All scales larger than this experience identical growth -- none are held back at any stage. Hence on scales larger than 220 Mly, the form of P(k) is just its primordial one. The next two figures clarify this.

 

Growth of P(k) for different comoving wavelengths.
 Resulting P(k) and its evolution
Left Figure shows the way in which perturbations grow for various wavelengths. An extended set of examples is shown, including the four from the first figure. Red curves apply to comoving scales that cross the horizon during the radiation era, and so suffer a reduction in their growth. The black curves apply to comoving scales that cross the horizon during the matter era, and so avoid any pause in growth.

Notice how the black curves preserve their "order" -- decreasing comoving wavelengths of 105, 104, 103 Mly have increasing P(k) at early times, as they do at late times (now). However, the red curves reverse their order: decreasing wavelengths 102, 101, 100 Mly have increasing P(k) at early times (just as they should), but the early entry of the smaller wavelengths freezes them, and reverses their order, so that decreasing wavelengths have decreasing P(k) at late times. Clearly, as a function of wavelength, P(k) will increase with decreasing wavelength at very large wavelengths, reach a peak at the wavelength which just avoids entering the horizon at equality, and then decrease rapidly with further decreasing wavelengths.

Right Figure shows this effect. The top curve is for the present time, while the other curves are for earlier times. We find that the evolved P(k) differs significantly from the initial P(k). They are similar at wavelengths greater than the horizon size at equality, but below that scale, P(k) falls rapidly as k-3 for ever smaller scales. A peak appears in P(k) at a comoving scale equal to the horizon at equality. Since equality occured at z ~ 3700 and time ~ 57 kyr, then the comoving scale is 3700 × 0.057 210 Mly. Let's now compare this with the observed data.

 

This Figure shows the SDSS galaxy P(k) with a detailed model best fit (red line). Notice that the range of length scales plotted is much smaller than in my diagrams -- it is only 1.6 dex, located just to the right of the peak.

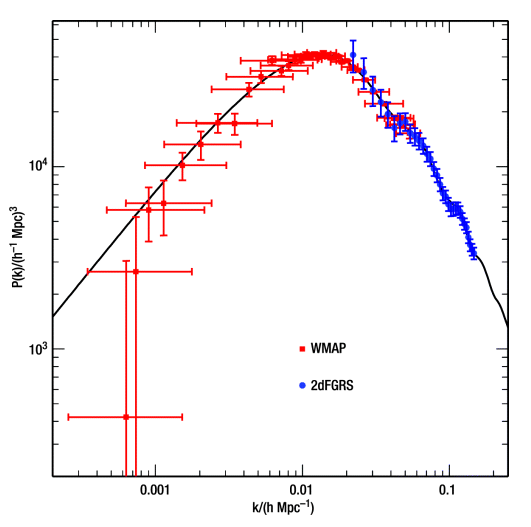
First, although this data doesn't identify the peak well, its scale is roughly as expected: ~few × 100 Mly.

Second, notice the slight wiggles in the calculated P(k) -- these are relics from the baryon acoustic peaks which grew prior to recombination. Their amplitude is greatly reduced since that early time, but they have now been seen in the sloan and 2dF data. They are called "Baryon Oscillations".

Third, notice that the gradient is significantly less then our simple model -- more like P(k) k-1 rather than k-3. This arises because there is some growth in the radiation era -- not zero as in our toy model (see below).

 

Left Figure below introduces more realistic growth during the radiation era. Growth doesn't end abruptly on horizon entry, but decays slowly as expansion velocity differences are redshifted away to nothing. Also, growth begins before the end of the radiation era as the matter component becomes more dominant. These two processes are approximated (faked) by quadratics of 1 dex width which smoothly match the growth rates before horizon entry (2) and after equality (4/3).

Right Figure Below shows the resulting P(k). The modified growth in the radiation era leads to a much broader peak, with flatter local gradient on the short wavelength side of the peak -- roughly as observed. Unfortunately, it is difficult to verify the gradual change to k-3 at even shorter scales because non-linear clustering has occurred, which feeds power from large scales to smaller ones. The blue dashed line shows the result of using a sophisticated (CMBFAST type) simulation which confirms the more gently curving peak (though this still doesn't include non-linear growth on small scales).

Growth of P(k) with more reasonable radiation behaviour.

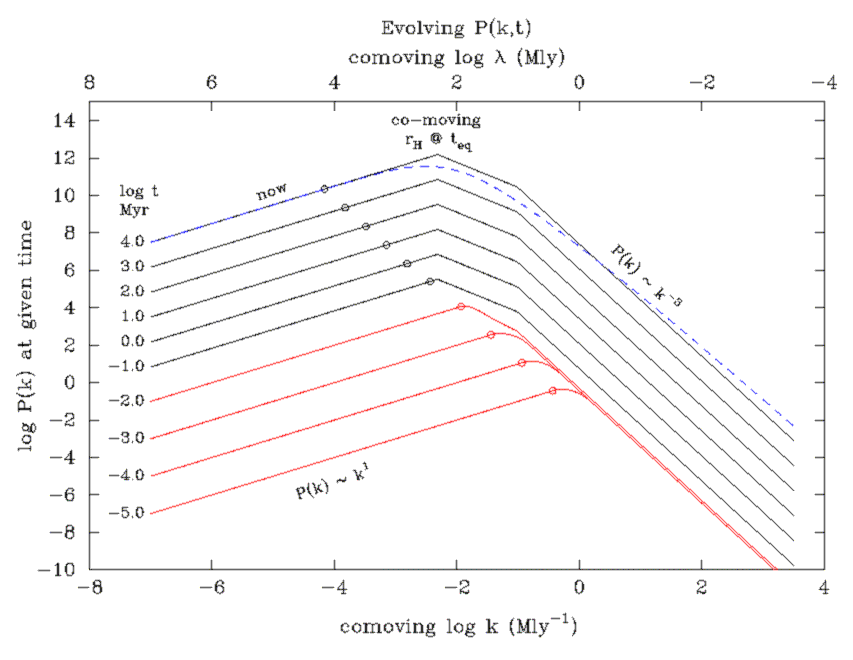
Resulting P(k) showing a broader peak