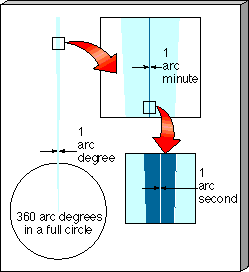
The size and scale of things are often specified by measuring lengths and angles. The concept of length measurement is fairly intuitive. We've already noted the dimensions of some objects found in the universe, ranging from subatomic particles with sizes of 10-15 m to whole galaxies with sizes of 1021 m or more. The concept of angular measurement may be less intuitive, but it too can become second nature if you remember a few simple facts. A full circle contains 360 arc degrees (or just 360°). Therefore, the half-circle that stretches from horizon to horizon, passing directly overhead and spanning the portion of the sky visible to one person at any one time, contains 180°. Each 1° increment can be further subdivided into fractions of an arc degree, called arc minutes; there are 60 arc minutes in 1 arc degree. Both the Sun and the Moon project an angular size of 30 arc minutes on the sky. Your little finger, held at arm's length, does just about the same, covering a small (actually, about 40 arc minutes) slice of the entire 180 arc degrees from horizon to horizon. Finally, an arc minute can be further sliced into 60 equal arc seconds. Put another way, an arc minute is 1/60 of an arc degree, and an arc second is 1/60  (1/60 = 1/3600 of an arc degree. An arc second is an extremely small unit of angular measure. It is, in fact, the angle subtended (projected) by a centimeter-sized object at a distance of about 2 kilometers or approximately the angle subtended by a dime when seen from a mile away. The accompanying figure illustrates this subdivision of the circle into progressively smaller units.
Don't be confused by the units used to measure angles. Arc minutes and arc seconds have nothing to do with the measurement of time, and arc degrees have nothing to do with temperature. Arc degrees, |
arc minutes, and arc seconds are simply ways to measure the size and position of objects in the universe. An arc degree is usually written as 1°, 1 arc minute is denoted by 1', and 1 arc second is 1".
The angular size of an object depends both on its actual size and on its distance from us. For example, the Moon, at its present distance from Earth, has an angular diameter of 0.5°, or 30'. If the Moon were twice as far away, it would appear half as big—15' across—even though its actual size would be the same. Similarly, if the Moon were one-third as far away, its angular diameter would be three times as great—1.5° and so on. Thus, angular size by itself is not enough to determine the actual diameter of an object—the distance must also be known.
|
MORE PRECISELY 1-1Angular Measure