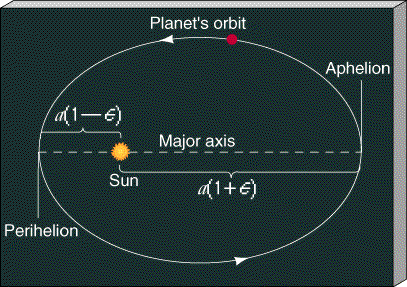
| Two numbers—semi-major axis and eccentricity—are all that are needed to describe the size and shape of a planet's orbital path. From them we can derive many other useful quantities. Two of the most important are the planet's perihelion (its point of closest approach to the Sun) and its aphelion (greatest distance from the Sun). From the definitions presented in the text, it follows that if the planet's orbit has semi-major axis a and eccentricity e, its perihelion is at a distance a(l—e) from the Sun, while its aphelion is at a(l + e). These points and distances are illustrated in the accompanying figure.
Note that while the Sun resides at one focus, the other focus is empty and has no particular significance. Thus, for example, a (hypothetical) planet with a semi-major axis of 400 million km and an eccentricity of 0.5 (the eccentricity of the |
ellipse shown in the diagram) would range between 400 No planet has an orbital eccentricity as large as 0.5—the planet with the most eccentric orbit is Pluto, with e= 0.248 (see Table 2.1). However, many meteoroids, and all comets (see Chapter 14) have eccentricities considerably greater than this. In fact, most comets visible from Earth have eccentricities very close to 1. Their highly elongated orbits approach within a few A.U. of the Sun at perihelion, yet these tiny frozen worlds spend most of their time far beyond the orbit of Pluto. |
 |
|