We can use Newtonian mechanics to calculate the relationship between the distance (r) and the speed (v) of a planet moving in a circular orbit around the Sun (of mass m). By calculating the force required to keep the planet moving in a circle and comparing it with the gravitational force due to the Sun, it can be shown that the circular speed is
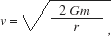
where the gravitational constant G is defined in More Precisely 2-2. Dividing this speed into the circumference of the orbit (2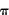 r), we obtain the modified form of Kepler's third law (equivalent to the formula presented in the text):
|
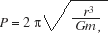
where P = 2 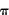r/v is the orbital period.
Because we have measured G in the laboratory on Earth and because we know the length of a year and the size of the astronomical unit, we can use Newtonian mechanics to weigh the Sun. Inserting the known values of v = 30 km/s, r = 1 A.U. = 1.5  1011 m, and G = 6.7 10-11 N m2/kg2in the equation, we can calculate the mass of the Sun to be 2.0 1030 kg—an enormous mass by terrestrial standards. Similarly, knowing the distance to the Moon and the length of the (sidereal) month, we can measure the mass of Earth to be 6.0 1024 kg.
In fact, this is how basically all masses are measured in astronomy. Because we can't just go out and weigh an astronomical object when we need to know its mass, we must look for its gravitational influence on something else. This principle applies to planets, stars, galaxies, and even clusters of galaxies—very different objects but all subject to the same physical laws. |
MORE PRECISELY 2-3 Weighing the Sun