Figure 3.1 shows a galaxy in the constellation Andromeda. On a dark, clear night, far from cities or other sources of light, the Andromeda Galaxy, as it is generally called, can be seen with the naked eye as a faint, fuzzy patch on the sky, comparable in diameter to the full Moon. Yet the fact that it is visible from Earth belies this galaxy's enormous distance from us. It lies roughly 3 million light years away. An object at such a distance is truly inaccessible in any realistic human sense. Even if a space probe could miraculously travel at the speed of light, it would need 3 million years to reach this galaxy and 3 million more to return with its findings. Considering that civilization has existed on Earth for fewer than 10,000 years (and its prospects for the next 10,000 are far from certain), even this unattainable technological feat would not provide us with a practical means of exploring other galaxies—or even the farthest reaches of our own, "only" a few tens of thousands of light years distant.
Figure 3.1 The pancake-shaped Andromeda Galaxy is almost 3 million light years away, according to the most recent distance measurements. It contains a few hundred billion stars.
Given the impossibility of traveling to such remote parts of the universe, how do astronomers know anything about objects far from Earth? How do we obtain detailed information about any planet, star, or galaxy too distant for a personal visit or any kind of controlled experiment? The answer is that we use the laws of physics, as we know them here on Earth, to interpret the electromagnetic radiation emitted by these objects. Radiation is any way in which energy is transmitted through space from one point to another without the need for any physical connection between those two locations. The term electromagnetic just means that the energy is carried in the form of rapidly fluctuating electric and magnetic fields (to be discussed in more detail later in Section 3.2). Virtually all we know about the universe beyond Earth's atmosphere has been gleaned from painstaking analysis of electromagnetic radiation received from afar. Visible light is the particular type of electromagnetic radiation to which our human eyes happen to be sensitive. As light enters our eye, the cornea and lens focus it onto the retina, whereupon small chemical reactions triggered by the incoming energy send electrical impulses to the brain, producing the sensation of sight. But there is also invisible electromagnetic radiation, which goes completely undetected by our eyes. Radio, infrared, and ultraviolet waves, as well as X rays and gamma rays, all fall into this category.
Recognize that, despite the different names, the words light, rays, radiation, and waves really all refer to the same thing. The names are just historical accidents, reflecting the fact that it took many years for scientists to realize that these apparently very different types of radiation are in reality one and the same physical phenomenon. Throughout this text, we will use the general terms "light" and "electromagnetic radiation" more or less interchangeably.
Despite the early confusion still reflected in the modern terminology, scientists now know that all types of electromagnetic radiation travel through space in the form of waves. To understand the behavior of light, then, we must know a little about wave motion.
Simply stated, a wave is a way in which energy is transferred from place to place without physical movement of material from one location to another. In wave motion, the energy is carried by a disturbance of some sort. This disturbance, whatever its nature, occurs in a distinctive repeating pattern. Ripples on the surface of a pond, sound waves in air, and electromagnetic waves in space, despite their many obvious differences, all share this basic defining property.
As a familiar example, imagine a twig floating in a pond. A pebble thrown into the pond at some distance from the twig disturbs the surface of the water, setting it into up-and-down motion. This disturbance will propagate outward from the point of impact in the form of waves. When the waves reach the twig, some of the pebble's energy will be imparted to it, causing the twig to bob up and down. In this way, both energy and information —the fact that the pebble entered the water—are transferred from the place where the pebble landed to the location of the twig. We could tell that a pebble (or, at least, some object) had entered the water just by observing the twig. With a little additional physics, we could even estimate the pebble's energy.
A wave is not a physical object. No water traveled from the point of impact of the pebble to the twig—at any location on the surface, the water surface simply moved up and down as the wave passed. What, then, did move across the surface of the pond? As illustrated in Figure 3.2, the answer is that the wave was the pattern of up-and-down motion, and it is this pattern that was transmitted from one point to the next as the disturbance moved across the water.
Figure 3.2 The passage of a wave across a pond causes the surface of the water to bob up and down, but there is no movement of water from one part of the pond to another. Here waves ripple out from the point where a pebble has hit the water to the point where a twig is floating. The inset shows schematically a cross section through part of the pond surface as the wave passes. The points numbered 1 through 5 represent nearby particles on the surface.
Figure 3.3 shows how wave properties are quantified and establishes some standard terminology. We characterize waves not only by the speed with which they move but also by the length of their cycle. How many seconds does it take for a wave to repeat itself at some point in space? This is its wave period. How many meters does it take for the wave to repeat itself at a given moment in time? This is its wavelength, defined as the length of an individual wave cycle. The wavelength can be measured as the distance between two adjacent wave crests, two adjacent wave troughs, or any other two similar points on adjacent wave cycles (such as the two points marked by an " " in the figure). The maximum departure of the wave from the undisturbed state—still air or the flat pond surface—is called its amplitude.
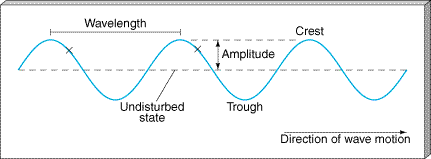
Figure 3.3 Representation of a typical wave, showing its direction of motion, wavelength, and amplitude.
If a wave moves at high speed, then the number of crests or cycles passing any given point per unit time—the wave's frequency—is high. Conversely, if a wave moves slowly, with only a few crests passing per unit time, we say that it has a low frequency. The frequency of a wave is just 1 divided by the wave's period:
Frequency is expressed in units of inverse time, or cycles per second, termed hertz (Hz) in honor of the nineteenth-century German scientist Heinrich Hertz, who studied the properties of radio waves. Thus, a wave having a period of 5 s, meaning that one wave crest passes any given point every 5 seconds, has a frequency of (1/5) cycles/s = (1/5) Hz = 0.2 Hz.
Wavelength and wave frequency are inversely related. Doubling the frequency halves the wavelength, halving the frequency doubles the wavelength, and so on. This inverse relationship is easily understood. For a given wave speed, if the wave crests are close together, then more of them pass by a given point each second; when the crests are far apart, few of them pass by per unit time. The wave speed is simply the product of the wavelength and the frequency:
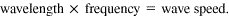
Put another way, a wave crest moves a distance equal to one wavelength in one wave period. For example, if the wave in our earlier example has a wavelength of 0.5 m, we can calculate its speed to be (0.5 m) (0.2 Hz) = 0.1 m/s.
Light exhibits two key properties that are characteristic of all forms of wave motion: diffraction and interference. Diffraction is the deflection, or "bending," of a wave as it passes a corner or moves through a narrow gap. As depicted in Figure 3.4, a sharp-edged hole in a barrier seems at first glance to produce a sharp shadow. Closer inspection, however, reveals that the shadow actually has a "fuzzy" edge. We are not normally aware of such effects in everyday life because diffraction is generally very small for visible light. For any wave, the amount of diffraction is proportional to the ratio of the wavelength to the width of the gap. The longer the wavelength and/or the smaller the gap, the greater the angle through which the wave is diffracted. Thus, visible light, with its extremely short wavelengths, shows perceptible diffraction only when passing through very narrow openings. (The effect is much more noticeable for sound waves, however—no one thinks twice about our ability to hear people even when they are around a corner and out of our line of sight.)
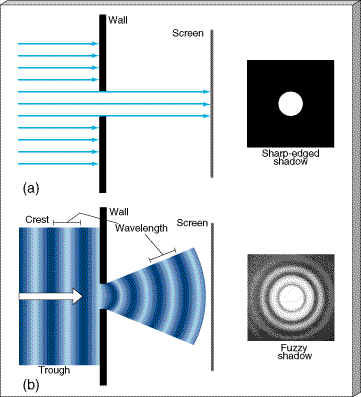
Figure 3.4 Diffraction of a light wave. (a) If radiation were composed of rays or particles moving in perfectly straight lines, no bending would occur as a beam of light passed through a circular hole in a barrier, and the outline of the hole, projected onto a screen, would have perfectly sharp edges. (b) In fact, light is diffracted through an angle that depends on the ratio of the wavelength of the wave to the size of the gap. The result is that the outline of the hole becomes "fuzzy," as shown in this actual photograph of the diffraction pattern produced by a small circular opening.
Interference is the ability of two or more waves to reinforce or cancel each other. Figure 3.5 shows two identical waves moving through the same region of space. In Figure 3.5(a) the waves are positioned so that their crests and troughs exactly coincide. The net effect is that the two wave motions reinforce each other, resulting in a wave of greater amplitude. This is known as constructive interference. In Figure 3.5(b) the two waves exactly cancel, so that no net motion remains. This is destructive interference. As with diffraction, interference between waves of visible light is not noticeable in everyday experience; however, it is easily measured in the laboratory.
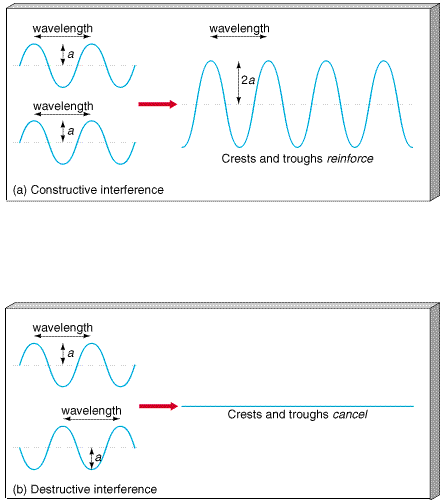
Figure 3.5 Interference of two identical waves: (a) constructive and (b) destructive. In constructive interference, the two waves (of amplitude a) reinforce each other to produce a larger-amplitude wave of the same wavelength. However, in destructive interference, the two waves exactly cancel out.
In the chapters that follow we will find that both diffraction and interference play important roles in many areas of observational astronomy.