As mentioned in Section 3.4, Wien's law relates the temperature T of an object to the wavelength 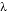 max at which it emits the most radiation (The Greek letter max at which it emits the most radiation (The Greek letter 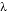 —lambda—is conventioanlly used to denote wavelength). Mathematically, if we measure T in kelvins and —lambda—is conventioanlly used to denote wavelength). Mathematically, if we measure T in kelvins and 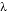 max in centimeters, we find that max in centimeters, we find that
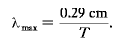
We could also convert Wien's law into a statement about frequency (f), using the relation f = c/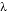 to obtain fmax = 1.0 to obtain fmax = 1.0  1011 THz. However, the law is most commonly stated in terms of wavelength and is probably easier to remember that way. Thus at 6000 K, the wavelength of maximum intensity is 0.29/6000 cm, or 480 nm, corresponding to the yellow-green part of the visible spectrum. (Recall that 1 nanometer—1 nm—is equal to 10-9 m; see Appendix 2.) 1011 THz. However, the law is most commonly stated in terms of wavelength and is probably easier to remember that way. Thus at 6000 K, the wavelength of maximum intensity is 0.29/6000 cm, or 480 nm, corresponding to the yellow-green part of the visible spectrum. (Recall that 1 nanometer—1 nm—is equal to 10-9 m; see Appendix 2.)
We can also give Stefan's law a more precise mathematical formulation. With T measured in kelvins, the total amount of energy emitted per square meter of its surface per second (a quantity known as the energy flux F) is given by |
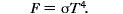
The constant 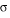 (the Greek letter sigma) is known as the Stefan-Boltzmann constant, or often just Stefan's constant, after Josef Stefan, the Austrian scientist who formulated the equation. (the Greek letter sigma) is known as the Stefan-Boltzmann constant, or often just Stefan's constant, after Josef Stefan, the Austrian scientist who formulated the equation.
The SI unit of energy is the joule (J). Probably more familiar is the closely related unit called the watt (W), which measures power—the rate at which energy is emitted or expended by an object. One watt is the emission of one joule per second; for example, a 100-W light bulb emits energy (mostly in the form of infrared and visible light) at a rate of 100 J/s. In these units, the Stefan-Boltzmann constant has the value
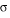 = 5.67 = 5.67  10-8 W/m2 10-8 W/m2 K4. K4.
Notice just how rapidly the energy flux increases with increasing temperature. A piece of metal in a furnace, when at a temperature of 3500 K, radiates energy at a rate of about 850 W for every square centimeter of its surface area. Doubling its temperature to 7000 K (so that it becomes yellow to white hot, by Wien's law) increases the energy emitted by a factor of 16 (four "doublings"), to 13.6 kilowatts (kW) (13,600 W) per square centimeter. |