| Most celestial objects rotate. Planets, moons, stars, and galaxies all have some angular momentum, which we can define as the tendency of a body to keep spinning or moving in a circle. Angular momentum is as important a property of an object as its mass or its energy.
Consider, first, a simpler motion—linear momentum, which is defined as the product of an object's mass and its speed:
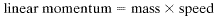
This is the tendency of an object to keep moving in a straight line in the absence of external forces. Consider a truck and a bicycle rolling equally fast down a street. Each has some linear momentum, but you would obviously find it easier to stop the less massive bicycle. Although the two vehicles have the same speed, the truck has more momentum. We see that the linear momentum of an object depends on the mass of that object. It also depends on the speed. If two bicycles were rolling down the street at different speeds, the slower one could be stopped more easily.
Angular momentum is an analogous property of objects that are rotating or revolving. However, in addition to mass and speed, the angular momentum also depends on the way in which the object's mass is distributed. The farther the mass is from the object's axis of rotation, the greater the angular momentum. For example, if you whirl a ball with constant speed at the end of a string, its angular momentum will depend directly on the length of the string—the longer the string, the greater the ball's angular momentum. We can therefore say, loosely, that
where "size" is a quantity that depends not only on the object's dimensions but also on the distribution of its mass. For the simple case of the ball on a string, it is just the length of the string (the radius of the ball's "orbit"). Note that the "speed" for linear momentum refers to motion in a straight line. For angular momentum, "speed" refers to spinning or orbital motion. |
According to Newton's laws of motion, both types of momentum—linear and angular—must be conserved at all times. In other words, both linear and angular momentum must remain constant before, during, and after a physical change in any object (so long as no external forces act). For example, if a spherical object having some spin begins to contract, the relationship above demands that it spin faster, so that the product mass  speed size remains constant. The sphere's mass does not change during the contraction, yet the size of the object clearly decreases. Its rotation speed must therefore increase in order to keep the total angular momentum unchanged.
Figure skaters use the principle of angular-momentum conservation. They spin faster by drawing in their arms (as shown in the accompanying figure) and slow down by extending them. Here the mass of the human body remains the same, but its lateral size changes, causing the body's circular speed to change to conserve angular momentum.
|
