| All the discussion of luminosity, brightness, and energy flux (Section 17.4) can equally well be written in terms of magnitudes. Here we present a little more detail on the "magnitude versions" of two important topics—stellar luminosity and the inverse-square law.
Recall that a star's absolute magnitude is the apparent magnitude we would measure if the star were located at a standard distance of 10 pc from us. Absolute magnitude is equivalent to luminosity—an intrinsic property of a star. Given that the Sun's absolute magnitude is 4.8, we can construct a "conversion chart" (shown at right) relating these two quantities. Since an increase in brightness by a factor of 100 corresponds, by definition, to a reduction of a star's magnitude by 5 units, it follows that a star with luminosity 100 times that of the Sun has absolute magnitude 4.8 - 5 = -0.2, and an 0.01 solar luminosity star has absolute magnitude 4.8 + 5 = 9.8. We can fill in the gaps by realizing that one magnitude corresponds to a factor of 1001/5 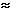 2.512, two magnitudes to 1002/5 2.512, two magnitudes to 1002/5 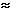 6.310, and so on. A factor of 10 in brightness corresponds to 2.5 magnitudes. You can use this chart to convert between solar luminosities and absolute magnitudes in many of the figures in this and later chapters. 6.310, and so on. A factor of 10 in brightness corresponds to 2.5 magnitudes. You can use this chart to convert between solar luminosities and absolute magnitudes in many of the figures in this and later chapters.
The inverse-square law can also be recast in these terms. Increasing the distance to a star by a factor of 10 decreases its energy flux by a factor of 100 (by the inverse square law) and hence increases its apparent magnitude by 5 units. Increasing the distance by a factor of 100 increases the apparent magnitude by 10. Since absolute magnitude is a measure of the energy flux received from a star at a distance of 10 pc, we can write:
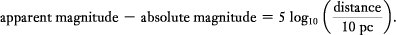
(The logarithm function is defined by the property that if a 5=log10(b), then b 5=10a.) The difference between the apparent and absolute magnitudes of an object is usually referred to as its distance modulus. In terms of distance modulus (DM), we can rewrite the preceding equation as:
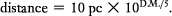
This doesn't look much like the inverse-square law presented in the text! Nevertheless, it contains exactly the same information, and it is in widespread use in this form throughout astronomy.

|