We can measure our Galaxy's mass by studying the motions of gas clouds and stars in the Galactic disk. Recall from Chapter 2 that Kepler's third law (as modified by Newton) connects the orbital period, orbit size, and masses of any two objects in orbit around each other:
(Sec. 2.7)
As we saw earlier, the distance from the Sun to the Galactic center is about 8 kpc, and the Sun's orbital period is 225 million years. Substituting these numbers into the preceding equation, we obtain a mass of almost 1011 solar masses—100 billion times the mass of our Sun. The Milky Way Galaxy is truly enormous, in mass as well as in size.
But what mass have we just measured? When we performed the analogous calculation in the case of a planet orbiting the Sun (Section 1.7), there was no ambiguity: neglecting the planet's mass, the result of our calculation was the mass of the Sun. However, the Galaxy's matter is not concentrated at the Galactic center (as the Sun's mass is concentrated at the center of the solar system); instead, Galactic matter is distributed over a large volume of space. Some of it lies inside the Sun's orbit (that is, within 8 kpc of the Galactic center), and some lies outside, at large distances from both the Sun and the center of the Galaxy. What portion of the Galaxy's mass controls the Sun's orbit? Isaac Newton answered this question three centuries ago: the Sun's orbital period is determined by the portion of the Galaxy that lies within the orbit of the Sun. This is the mass computed from the foregoing equation.
To determine the mass of the Galaxy on larger scales—that is, to find how much matter is contained within spheres of progressively larger radii—we must measure the orbital motion of stars and gas farther from the Galactic center than is the Sun. Astronomers have found that the most effective way to do this is to make radio observations of gas in the Galactic disk, because radio waves are relatively unaffected by interstellar absorption and allow us to probe to great distances, far beyond the Sun's orbit. On the basis of these studies, radio astronomers have determined our Galaxy's rotation rate at various distances from the Galactic center. The resultant plot of rotation speed versus distance from the center (Figure 23.19) is called the Galactic rotation curve.
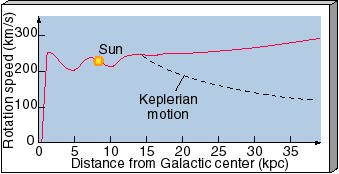
Figure 23.19 The rotation curve for the Milky Way Galaxy plots rotation speed versus distance from the Galactic center. We can use this curve to compute the mass of the Galaxy that lies within any given radius. The dashed curve is the rotation curve expected if the Galaxy "ended" abruptly at a radius of 15 kpc, the limit of most of the known spiral structure and the globular cluster distribution. The fact that the red curve does not follow this dashed line, but instead stays well above it, indicates that there must be additional matter beyond that radius.
Knowing the Galactic rotation curve, we can now repeat our earlier calculation to compute the total mass that lies within any given distance from the Galactic center. We find, for example, that the mass within about 15 kpc from the center—the volume defined by the globular clusters and the known spiral structure—is roughly 2 1011 solar masses, about twice the mass contained within the Sun's orbit. Does the distribution of matter in the Galaxy "cut off" at this point, where the luminosity drops off sharply? Surprisingly, it does not.
If most of the matter in the Galaxy were contained within the edge of the visible structure, Newton's laws of motion predict that the orbital speed of stars and gas beyond 15 kpc would decrease with increasing distance from the Galactic center, just as the orbital speeds of the planets diminish as we move outward from the Sun. The dashed line in Figure 23.19 indicates what the rotation curve would look like in that case. However, the true rotation curve is quite different. Far from falling off at larger distances, it rises slightly out to the limits of our measurement capabilities. This implies that the amount of mass contained within successively larger radii continues to grow beyond the orbit of the Sun, apparently out to a distance of at least 40 or 50 kpc. According to the preceding equation, the amount of mass within 40 kpc is approximately 6 1011 solar masses. Since 2
1011 solar masses lies within 15 kpc of the Galactic center, we have to conclude that at least twice as much mass lies outside the luminous part of our galaxy—the part made up of stars, star clusters, and spiral arms—as lies inside!
Based on these observations of the Galactic rotation curve, astronomers now believe that the luminous portion of the Milky Way Galaxy—the region outlined by the globular clusters and by the spiral arms—is merely the "tip of the Galactic iceberg." Our Galaxy is in reality very much larger. The luminous region is surrounded by an extensive, invisible dark halo, which dwarfs the inner halo of stars and globular clusters and extends well beyond the 15-kpc radius once thought to represent the limit of our Galaxy. But what is the composition of this dark halo? We do not detect enough stars or interstellar matter to account for the mass that our computations tell us must be there. We are inescapably drawn to the conclusion that most of the mass in our Galaxy exists in the form of invisible dark matter, which we presently simply do not understand.
The term dark here does not refer just to matter undetectable in visible light. The material has (so far) escaped detection at all wavelengths, from radio to gamma rays. Only by its gravitational pull do we know of its existence. Dark matter is not hydrogen gas (atomic or molecular), nor is it made up of ordinary stars. Given the amount of matter that must be accounted for, we would have been able to detect it with present-day equipment if it were in either of those forms. Its nature and its consequences for the evolution of galaxies and the universe are among the most important questions in astronomy today.
Many candidates have been suggested for this dark matter, although none is proven. Black holes may supply some of the unseen mass, although their very existence is still debated, and very few candidates exist. (Sec. 22.7) However, given that black holes are the evolutionary products of (relatively rare) massive stars, it is unlikely that there could be enough of them to hide large amounts of Galactic matter. Currently among the strongest "stellar" contenders are brown dwarfs—low-mass prestellar objects that never reached the point of core nuclear burning—white dwarfs, and faint, low-mass red dwarfs.
(Secs. 19.3, 20.3) These objects could in principle exist in great numbers throughout the Galaxy yet would be exceedingly hard to see.
Recent Hubble Space Telescope observations of globular clusters seem to argue against at least the last of these possibilities. Figure 23.20 shows a Hubble image of a relatively nearby globular cluster—one close enough that very faint red dwarfs could have been detected if any existed. The Hubble data suggest that there is a cutoff at about 0.2 solar masses, below which stars form much less frequently than had previously been supposed. As a result, very low-mass stars seem to be unexpectedly rare in our Galaxy.

Figure 23.20 Very sensitive visible observations with the Hubble Space Telescope have apparently ruled out faint red-dwarf stars as candidates for dark matter. The object shown here, the globular cluster NGC 6397, is one of many regions searched in the Milky Way. The inset, 0.4 pc on a side, shows a high-resolution Hubble view. The scores of diamonds have been overlaid at positions where red dwarfs might (statistically) have been expected if they did indeed make up the dark matter, but they were not found.
A radically different alternative is that the dark matter is made up of exotic subatomic particles that pervade the entire universe. Many theoretical astrophysicists believe that these particles could have been produced in abundance during the very earliest moments of our universe. If the particles have survived to the present day, there might be enough of them to account for all the dark matter we believe must be out there. This idea is hard to test, however, because any particles of this nature that might exist would be very hard to detect. Several detection experiments have been attempted, so far without success.
Recently, researchers have obtained insight into the distribution of stellar dark matter by using a key element of Albert Einstein's theory of general relativity—the prediction that a beam of light can be deflected by a gravitational field, which has already been verified in the case of starlight that passes close to the Sun (More Precisely 22-2). Although this effect is small, it has the potential for making otherwise invisible stellar objects observable from Earth. Here's how.
Imagine looking at a distant star as a faint foreground object (such as a brown dwarf or a white dwarf) happens to cross your line of sight. As illustrated in Figure 23.21, the intervening object deflects a little more starlight than usual toward you, resulting in a temporary, but quite substantial, brightening of the distant star. In some ways, the effect is like the focusing of light by a lens, and the process is known as gravitational lensing. The foreground object is referred to as a gravitational lens. The amount of brightening and the duration of the effect depend on the mass, distance, and speed of the lensing object. Typically, the apparent brightness of the background star increases by a factor of 2 to 5 for a period of several weeks. Thus, even though the foreground object cannot be seen directly, its effect on the light of the background star makes it detectable. (In Chapter 25 we will encounter other instances of gravitational lensing in the universe, but on very much larger scales.)

Figure 23.21 Gravitational lensing by a faint foreground object (such as a brown dwarf) can temporarily cause a background star to brighten significantly, providing a means of detecting otherwise invisible stellar dark matter.
Of course, the probability that one star will pass almost directly in front of another, as seen from Earth, is extremely small. But by observing millions of stars every few days over a period of years (using automated telescopes and high-speed computers to reduce the burden of coping with so much data), astronomers have been able to see enough of these events to let them estimate the amount of stellar dark matter in the Galactic halo. The technique represents an exciting new means of probing the structure of our Galaxy. The first lensing events were reported in late 1993. Subsequent observations are consistent with lensing by low-mass white dwarfs and suggest that such stars could account for at least half of the dark matter inferred from dynamical studies.
Bear in mind, though, that the identity of the dark matter is not necessarily an all-or-nothing proposition. It is perfectly conceivable that more than one type of dark matter exists. For example, it is quite possible that most of the dark matter in the inner (visible) parts of galaxies is in the form of brown dwarfs and very-low-mass stars, while the dark matter farther out may be primarily in the form of exotic particles. We will return to this perplexing problem in later chapters.