|
【背景介绍】
霍尔效应是导电材料中的电流与磁场相互作用而产生电动势的效应。1879年美国霍普金斯大学研究生霍尔(Hall,
Edwin Herbert, 1855-1938)在研究金属导电机构时发现了这种电磁现象,故称霍尔效应(Hall
Effect)。后来曾有人利用霍尔效应制成测量磁场的磁传感器,但因金属的霍尔效应太弱而未能得到实际应用。随着半导体材料和制造工艺的发展,人们又利用半导体材料制成霍尔元件,由于它的霍尔效应显著而得到实用和发展,现在广泛用于非电量检测、电动控制、电磁测量和计算装置方面。在电流体中的霍尔效应也是目前在研究中的“磁流体发电”的理论基础。近年来,霍尔效应实验不断有新发现。1980年原西德物理学家冯·克利青(K.Von
Klitzing)研究二维电子气系统的输运特性,在低温和强磁场下发现了量子霍尔效应,这是凝聚态物理领域最重要的发现之一。目前对量子霍尔效应正在进行深入研究,并取得了重要应用,例如用于确定电阻的自然基准,可以极为精确地测量光谱精细结构常数等。
在磁场、磁路等磁现象的研究和应用中,霍尔效应及其元件是不可缺少的,利用它观测磁场直观、干扰小、灵敏度高、效果明显。
【实验目的】
1、了解霍尔效应原理及测量霍尔元件有关参数.
2、测绘霍尔元件的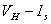 , ,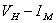 曲线了解霍尔电势差 曲线了解霍尔电势差 与霍尔元件控制(工作)电流 与霍尔元件控制(工作)电流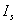 、励磁电流 、励磁电流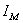 之间的关系。 之间的关系。
3、学习利用霍尔效应测量磁感应强度B及磁场分布。
4、判断霍尔元件载流子的类型,并计算其浓度和迁移率。
 5、学习用“对称交换测量法”消除负效应产生的系统误差。
5、学习用“对称交换测量法”消除负效应产生的系统误差。
【实验原理】
霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力的作用而引起的偏转。当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷在不同侧的聚积,从而形成附加的横向电场。
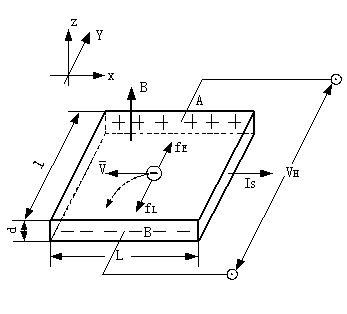
如右图(1)所示,磁场B位于Z的正向,与之垂直的半导体薄片上沿X正向通以电流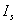 (称为控制电流或工作电流),假设载流子为电子(N型半导体材料),它沿着与电流 (称为控制电流或工作电流),假设载流子为电子(N型半导体材料),它沿着与电流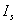 相反的X负向运动。 相反的X负向运动。
由于洛伦兹力 的作用,电子即向图中虚线箭头所指的位于y轴负方向的B侧偏转,并使B侧形成电子积累,而相对的A侧形成正电荷积累。与此同时运动的电子还受到由于两种积累的异种电荷形成的反向电场力 的作用,电子即向图中虚线箭头所指的位于y轴负方向的B侧偏转,并使B侧形成电子积累,而相对的A侧形成正电荷积累。与此同时运动的电子还受到由于两种积累的异种电荷形成的反向电场力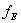 的作用。随着电荷积累量的增加, 的作用。随着电荷积累量的增加,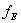 增大,当两力大小相等(方向相反)时, 增大,当两力大小相等(方向相反)时, =- =-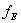 ,则电子积累便达到动态平衡。这时在A、B两端面之间建立的电场称为霍尔电场 ,则电子积累便达到动态平衡。这时在A、B两端面之间建立的电场称为霍尔电场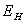 ,相应的电势差称为霍尔电压 ,相应的电势差称为霍尔电压 。 。
设电子按均一速度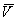 向图示的X负方向运动,在磁场B作用下,所受洛伦兹力为 向图示的X负方向运动,在磁场B作用下,所受洛伦兹力为 =-e =-e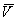 B B
式中e为电子电量,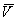 为电子漂移平均速度,B为磁感应强度。 为电子漂移平均速度,B为磁感应强度。
同时,电场作用于电子的力为
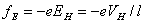
式中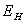 为霍尔电场强度, 为霍尔电场强度, 为霍尔电压, 为霍尔电压,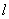 为霍尔元件宽度 为霍尔元件宽度
当达到动态平衡时,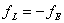
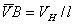 (1) (1)
设霍尔元件宽度为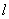 ,厚度为d,载流子浓度为n,则霍尔元件的控制(工作)电流为 ,厚度为d,载流子浓度为n,则霍尔元件的控制(工作)电流为
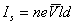 (2) (2)
由(1),(2)两式可得
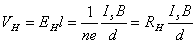 (3) (3)
即霍尔电压 (A、B间电压)与Is、B的乘积成正比,与霍尔元件的厚度成反比,比例系数 (A、B间电压)与Is、B的乘积成正比,与霍尔元件的厚度成反比,比例系数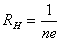 称为霍尔系数,它是反映材料霍尔效应强弱的重要参数,根据材料的电导率σ=neμ的关系,还可以得到: 称为霍尔系数,它是反映材料霍尔效应强弱的重要参数,根据材料的电导率σ=neμ的关系,还可以得到:
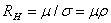 (4) (4)
式中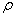 为材料的电阻率、μ为载流子的迁移率,即
单位电场下载流子的运动速度,一般电子迁移率大于空穴迁移率,因此制作霍尔元件时大多采用N型半导体材料。 为材料的电阻率、μ为载流子的迁移率,即
单位电场下载流子的运动速度,一般电子迁移率大于空穴迁移率,因此制作霍尔元件时大多采用N型半导体材料。
当霍尔元件的材料和厚度确定时,设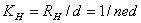 (5)
(5)
将式(5)代入式(3)中得
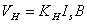 (6) (6)
式中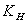 称为元件的灵敏度,它表示霍尔元件在单位磁感应强度和单位控制电流下的霍尔电势大小,其单位是[ 称为元件的灵敏度,它表示霍尔元件在单位磁感应强度和单位控制电流下的霍尔电势大小,其单位是[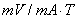 ],一般要求 ],一般要求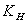 愈大愈好。 愈大愈好。
若需测量霍尔元件中载流子迁移率μ,则有
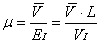 (7) (7)
将(2)式、(5)式、(7)式联立求得
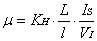 (8) (8)
其中VI为垂直于IS方向的霍尔元件两侧面之间的电势差,EI为由VI产生的电场强度,L、l分别为霍尔元件长度和宽度。
由于金属的电子浓度n很高,所以它的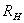 或 或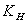 都不大,因此不适宜作霍尔元件。此外元件厚度d愈薄, 都不大,因此不适宜作霍尔元件。此外元件厚度d愈薄,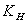 愈高,所以制作时,往往采用减少d的办法来增加灵敏度,但不能认为d愈薄愈好,因为此时元件的输入和输出电阻将会增加,这对锗元件是不希望的。 愈高,所以制作时,往往采用减少d的办法来增加灵敏度,但不能认为d愈薄愈好,因为此时元件的输入和输出电阻将会增加,这对锗元件是不希望的。
 应当注意,当磁感应强度B和元件平面法线成一角度时(如图2),作用在元件上的有效磁场是其法线方向上的分量 应当注意,当磁感应强度B和元件平面法线成一角度时(如图2),作用在元件上的有效磁场是其法线方向上的分量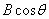 ,此时 ,此时
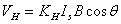 (9)
(9)
所以一般在使用时应调整元件两平面方位,使 达到最大,即θ=0, 达到最大,即θ=0, = =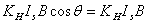
由式(9)可知,当控制(工作)电流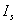 或磁感应强度B,两者之一改变方向时,霍尔电压 或磁感应强度B,两者之一改变方向时,霍尔电压 的方向随之改变;若两者方向同时改变,则霍尔电压 的方向随之改变;若两者方向同时改变,则霍尔电压 极性不变。 极性不变。
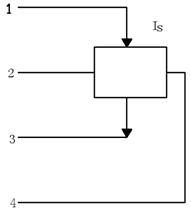
霍尔元件测量磁场的基本电路如图3,将霍尔元件置于待测磁场的相应位置,并使元件平面与磁感应强度B垂直,在其控制端输入恒定的工作电流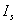 ,霍尔元件的霍尔电压输出端接毫伏表,测量霍尔电势 ,霍尔元件的霍尔电压输出端接毫伏表,测量霍尔电势 的值。 的值。
【实验仪器简介】
本套仪器由ZKY-HS霍尔效应实验仪和ZKY-HC霍尔效应测试仪两大部分组成。

霍尔效应螺线管磁场测试仪


螺线管磁场测试仪(左)和霍尔效应测试仪(右)
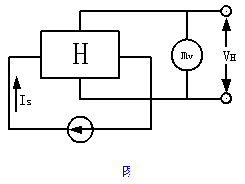
一、ZKY-HS霍尔效应实验仪
本实验仪由电磁铁、二维移动标尺、三个换向闸刀开关、霍尔元件及引线组成。
1、C型电磁铁
电磁铁线包绕向见右图。
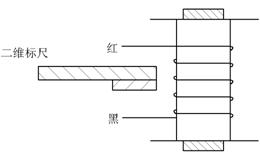
2、二维移动标尺及霍尔元件
水平标尺0—50mm
纵向标尺0—30mm
霍尔元件材料:
N型砷化镓
长度L: 300 宽度l: 100
宽度l: 100 厚度d: 2
厚度d: 2
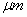
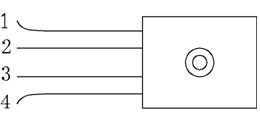
霍尔片上有4只引脚,其中编号为1、2的两只为霍尔工作电流端,编号为3、4的两只为霍尔电压输出端,同时将这4只引脚焊接在玻璃丝布板上,然后引到仪器换向闸刀开关上,能方便地进行实验(具体位置关系见图示)。
霍尔元件灵敏度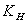 (mV/mA·T)、霍尔元件不等位电势V。每台实验仪面板上用标牌标示。 (mV/mA·T)、霍尔元件不等位电势V。每台实验仪面板上用标牌标示。
3、三个双刀双掷闸刀开关分别对励磁电流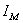 ,工作(控制)电流 ,工作(控制)电流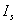 、霍尔电势 、霍尔电势 进行通断和换向控制。 进行通断和换向控制。
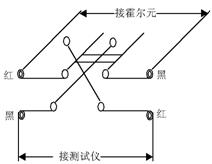
二、ZKY-HC霍尔效应测试仪
仪器背部为220V交流电源插座及保险丝。
仪器面板分为三大部分
1、励磁电流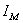 输出:前面板右侧 输出:前面板右侧
三位半数码管显示输出电流值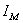 (mA) (mA)
输出直流恒流可调0000——1000mA(用调节旋纽调节)。
2、霍尔元件工作(控制)电流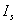 输出:前面板左侧 输出:前面板左侧
三位半数码管显示输出电流值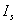 (mA) (mA)
输出直流恒流可调1.50——10.00mA(用调节旋纽调节)
注意:只有在接通负载时,恒流源才能输出电流,数显表上才有相应显示。
以上两组恒流源只能在规定的负载范围内恒流,与之配套的“实验仪”上的负载符合要求。若要作他用须注意。
3、霍尔电压 输入:前面板中部 输入:前面板中部
四位数码管显示输入电压值 (mV) (mV)
测量范围:
±199.9mV
若要测量交流磁场和研究交流工作电流对霍尔元件的影响等,则必须另外提供有效值与以上直流恒流源相近的交流电源,方可进行实验。
【实验注意事项】
1、霍尔元件及二维移动标尺易于折断、变形等损坏,应注意避免受挤压,碰撞等。实验前应检查两者及电磁铁是否松动、移位,并加以调整。
2、霍尔电压 测量的条件是霍尔元件平面与磁感应强度B垂直,此时 测量的条件是霍尔元件平面与磁感应强度B垂直,此时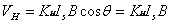 ,即 ,即 取得最大值,仪器在组装时已调整好,为防止搬运,移动中发生的形变、位移,实验前应将霍尔元件移至电磁铁气隙中心,调整霍尔元件方位,使其在 取得最大值,仪器在组装时已调整好,为防止搬运,移动中发生的形变、位移,实验前应将霍尔元件移至电磁铁气隙中心,调整霍尔元件方位,使其在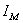 , ,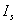 固定时,达到输出 固定时,达到输出 最大。 最大。
3、为了不使电磁铁过热而受到损害,或影响测量精度,除在短时间内读取有关数据,通以励磁电流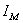 外,其余时间最好断开励磁电流开关。 外,其余时间最好断开励磁电流开关。
4、仪器不宜在强光照射下,高温、强磁场和有腐蚀气体的环境下工作和存放。
【实验项目】
一、研究霍尔效应及霍尔元件特性
1、
测量霍尔元件灵敏度KH,计算载流子浓度n(选做)。
2、
测定霍尔元件的载流子迁移率μ。
3、
判定霍尔元件半导体类型(P型或N型)或者反推磁感应强度B的方向。
4、研究 与励磁电流 与励磁电流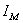 、工作(控制)电流IS之间的关系 、工作(控制)电流IS之间的关系
二、测量电磁铁气隙中磁感应强度B的大小以及分布
1、测量一定IM条件下电磁铁气隙中心的磁感应强度B的大小。
2、测量电磁铁气隙中磁感应强度B的分布
【实验方法与步骤】
一、按仪器面板上的文字和符号提示将ZKY-HS霍尔效应实验仪与ZKY-HC霍尔效应测试仪正确连接。
1、ZKY-HC霍尔效应测试仪面板右下方为提供励磁电流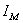 的恒流源输出端(0-1000mA),接霍尔效应实验仪上电磁铁线圈电流的输入端(将接线叉口与接线柱连接)。 的恒流源输出端(0-1000mA),接霍尔效应实验仪上电磁铁线圈电流的输入端(将接线叉口与接线柱连接)。
2、“测试仪”左下方为提供霍尔元件控制(工作)电流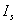 的恒流源(1.50-10.00mA) 的恒流源(1.50-10.00mA)
输出端,接“实验仪”霍尔元件工作电流输入端(将插头插入插座)。
3、“实验仪”上霍尔元件的霍尔电压VH输出端,接“测试仪”中部下方的霍尔电压输入端。
4、将测试仪与220V交流电源接通。
二、研究霍尔效应与霍尔元件特性
1、
测量霍尔元件灵敏度KH,计算载流子浓度n。
(若实验室配备有特斯拉计,可选做此实验)。
(1)调节励磁电流IM为0.8A,使用特斯拉计测量此时气隙中心磁感应强度B的大小。
(2)移动二维标尺,使霍尔元件处于气隙中心位置。
(3)调节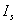 =2.00……、10.00mA(数据采集间隔1.00mA),记录对应的霍尔电压VH填入表(1),描绘IS—VH关系曲线,求得斜率K1(K1=VH/IS)。 =2.00……、10.00mA(数据采集间隔1.00mA),记录对应的霍尔电压VH填入表(1),描绘IS—VH关系曲线,求得斜率K1(K1=VH/IS)。
(4)据式(6)可求得KH,据式(5)可计算载流子浓度n。
2、
测定霍尔元件的载流子迁移率μ。
(1)调节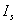 =2.00……、10.00mA(间隔为1.00mA),记录对应的输入电压降VI填入表4,描绘IS—VI关系曲线,求得斜率K2(K2=IS/VI)。 =2.00……、10.00mA(间隔为1.00mA),记录对应的输入电压降VI填入表4,描绘IS—VI关系曲线,求得斜率K2(K2=IS/VI)。
(2)若已知KH、L、l,据(8)式可以求得载流子迁移率μ。
3、
判定霍尔元件半导体类型(P型或N型)或者反推磁感应强度B的方向
(1)根据电磁铁线包绕向及励磁电流IM的流向,可以判定气隙中磁感应强度B的方向。
(2)根据换向闸刀开关接线以及霍尔测试仪IS输出端引线,可以判定IS在霍尔元件中的流向。
(3)根据换向闸刀开关接线以及霍尔测试仪VH输入端引线,可以得出VH的正负与霍尔片上正负电荷积累的对应关系
(4)由B的方向、IS流向以及VH的正负并结合霍尔片的引脚位置可以判定霍尔元件半导体的类型(P型或N型)。反之,若已知IS流向、VH的正负以及霍尔元件半导体的类型,可以判定磁感应强度B的方向。
4、测量霍尔电压 与励磁电流 与励磁电流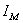 的关系 的关系
霍尔元件仍位于气隙中心,调节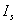 =10.00mA,调节 =10.00mA,调节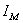 =100、200……1000mA(间隔为100mA),分别测量霍尔电压 =100、200……1000mA(间隔为100mA),分别测量霍尔电压 值填入表(2),并绘出 值填入表(2),并绘出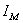 - - 曲线,验证线性关系的范围,分析当 曲线,验证线性关系的范围,分析当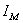 达到一定值以后, 达到一定值以后,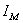 - - 直线斜率变化的原因。 直线斜率变化的原因。
三、测量电磁铁气隙中磁感应强度B的大小及分布情况
1、
测量电磁铁气隙中磁感应强度B的大小
(1)调节励磁电流IM为0—1000mA范围内的某一数值。
(2)移动二维标尺,使霍尔元件处于气隙中心位置。
(3)调节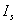 =2.00……、10.00mA(数据采集间隔1.00mA),记录对应的霍尔电压VH填入表(1),描绘IS—VH关系曲线,求得斜率K1(K1=VH/IS)。 =2.00……、10.00mA(数据采集间隔1.00mA),记录对应的霍尔电压VH填入表(1),描绘IS—VH关系曲线,求得斜率K1(K1=VH/IS)。
(4)将给定的霍尔灵敏度KH及斜率K1代入式(6)可求得磁感应强度B的大小。
(若实验室配备有特斯拉计,可以实测气隙中心B的大小,与计算的B值比较。)
2、考察气隙中磁感应强度B的分布情况
⑴、将霍尔元件置于电磁铁气隙中心,调节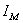 =1000mA, =1000mA,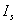 =10.00mA,测量相应的 =10.00mA,测量相应的 。 。
⑵、将霍尔元件从中心向边缘移动每隔5mm选一个点测出相应的 ,填入表3。 ,填入表3。
⑶、由以上所测 值,由式(6)计算出各点的磁感应强度,并绘出B-X图,显示出气隙内B的分布状态。 值,由式(6)计算出各点的磁感应强度,并绘出B-X图,显示出气隙内B的分布状态。
为了消除附加电势差引起霍尔电势测量的系统误差,一般按±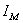 ,± ,±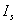 的四种组合测量求其绝对值的平均值。 的四种组合测量求其绝对值的平均值。
表1
VH-IS
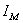 =800mA =800mA
|
Is(mA) |
V1(mV) |
V2(mV) |
V3(mV) |
V4(mV) |
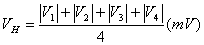 |
|
+IM+Is |
-IM+Is |
-IM-Is |
+IM-Is |
|
2.00 |
|
|
|
|
|
|
3.00 |
|
|
|
|
|
|
…… |
|
|
|
|
|
|
…… |
|
|
|
|
|
|
10.00 |
|
|
|
|
|
表2
VH-IS
Is=10.00mA
|
IM(mA) |
V1(mV) |
V2(mV) |
V3(mV) |
V4(mV) |
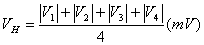 |
|
+IM+Is |
-IM+Is |
-IM-Is |
+IM-Is |
|
100 |
|
|
|
|
|
|
200 |
|
|
|
|
|
|
300 |
|
|
|
|
|
|
…… |
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
表3
VH-X
IM=1000mA
Is=10.00mA
|
X(mm) |
V1(mV) |
V2(mV) |
V3(mV) |
V4(mV) |
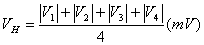 |
|
+IM+Is |
-Iμ+Is |
-Iμ-Is |
+IM-Is |
|
0 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
∶
∶ |
|
|
|
|
|
表4
IS-VI
【实验系统误差及其消除】
测量霍尔电势VH时,不可避免地会产生一些副效应,由此而产生的附加电势叠加在霍尔电势上,形成测量系统误差,这些副效应有:
(1)不等位电势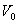
由于制作时,两个霍尔电势极不可能绝对对称地焊在霍尔片两侧(图5a)、霍尔片电阻率不均匀、控制电流极的端面接触不良(图5b)都可能造成A、B两极不处在同一等位面上,此时虽未加磁场,但A、B间存在电势差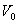 ,此称不等位电势, ,此称不等位电势,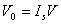 ,V是两等位面间的电阻,由此可见,在V确定的情况下, ,V是两等位面间的电阻,由此可见,在V确定的情况下,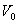 与 与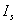 的大小成正比,且其正负随 的大小成正比,且其正负随 的方向而改变。 的方向而改变。
(2)爱廷豪森效应

当元件的X方向通以工作电流 ,Z方向加磁场B时,由于霍尔片内的载流子速度服从统计分布,有快有慢。在达到动态平衡时,在磁场的作用下慢速与快速的载流子将在洛伦兹力和霍尔电场的共同作用下,沿y轴分别向相反的两侧偏转,这些载流子的动能将转化为热能,使两侧的温升不同,因而造成y方向上的两侧的温差(TA-TB)。 ,Z方向加磁场B时,由于霍尔片内的载流子速度服从统计分布,有快有慢。在达到动态平衡时,在磁场的作用下慢速与快速的载流子将在洛伦兹力和霍尔电场的共同作用下,沿y轴分别向相反的两侧偏转,这些载流子的动能将转化为热能,使两侧的温升不同,因而造成y方向上的两侧的温差(TA-TB)。
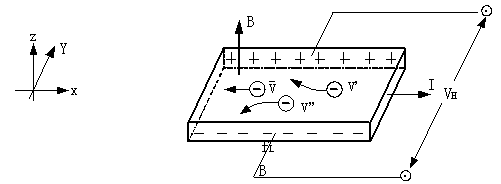
图6
正电子运动平均速度 图中
因为霍尔电极和元件两者材料不同,电极和元件之间形成温差电偶,这一温差在A、B间产生温差电动势VE,VE∝IB
这一效应称爱廷豪森效应,VE的大小与正负符号与I、B的大小和方向有关,跟VH与I、B的关系相同,所以不能在测量中消除。
(3)伦斯脱效应
由于控制电流的两个电极与霍尔元件的接触电阻不同,控制电流在两电极处将产生不同
的焦耳热,引起两电极间的温差电动势,此电动势又产生温差电流(称为热电流)Q,热电流在磁场作用下将发生偏转,结果在y方向上产生附加的电势差 且 且
VN∝QB这一效应称为伦斯脱效应,由上式可知 的符号只与B的方向有关。 的符号只与B的方向有关。
(4)里纪—勒杜克效应
如(3)所述霍尔元件在X方向有温度梯度 ,引起载流子沿梯度方向扩散而有热电 ,引起载流子沿梯度方向扩散而有热电
流Q通过元件,在此过程中载流子受Z方向的磁场B作用下,在y方向引起类似爱廷豪森效应的温差TA-TB,由此产生的电势差 ∝QB,其符号与B的的方向有关,与 ∝QB,其符号与B的的方向有关,与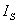 的方向无关。 的方向无关。
为了减少和消除以上效应引起的附加电势差,利用这些附加电势差与霍尔元件控制(工作)电流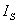 ,磁场B(既相应的励磁电流 ,磁场B(既相应的励磁电流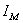 )的关系,采用对称(交换)测量法进行测量。 )的关系,采用对称(交换)测量法进行测量。
当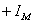 , ,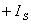 时 时
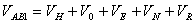
当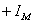 , ,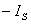 时 时
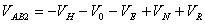
当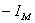 , ,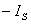 时 时
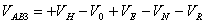
当 , , 时 时

对以上四式作如下运算则得:

可见,除爱廷豪森效应以外的其他副效应产生的电势差会全部消除,因爱廷豪森效应所产生的电势差 的符号和霍尔电势 的符号和霍尔电势 的符号,与 的符号,与 及B的方向关系相同,故无法消除,但在非大电流、非强磁场下, 及B的方向关系相同,故无法消除,但在非大电流、非强磁场下, >> >> ,因而 ,因而 可以忽略不计, 可以忽略不计,
 ≈ ≈  。 。
一般情况下,当 较大时, 较大时, 与 与 同号, 同号, 与 与 同号,而两组数据反号,故 同号,而两组数据反号,故

即用四次测量值的绝对值之和求平均值即可。
|