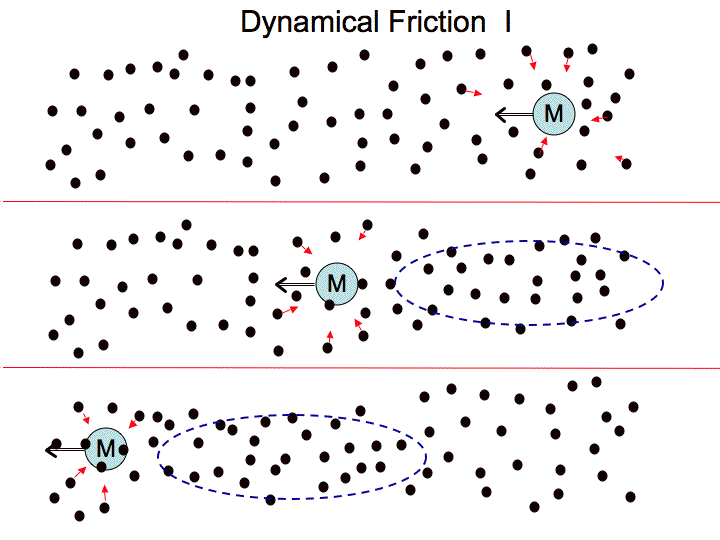
Basic Sketch of Retarding Wake
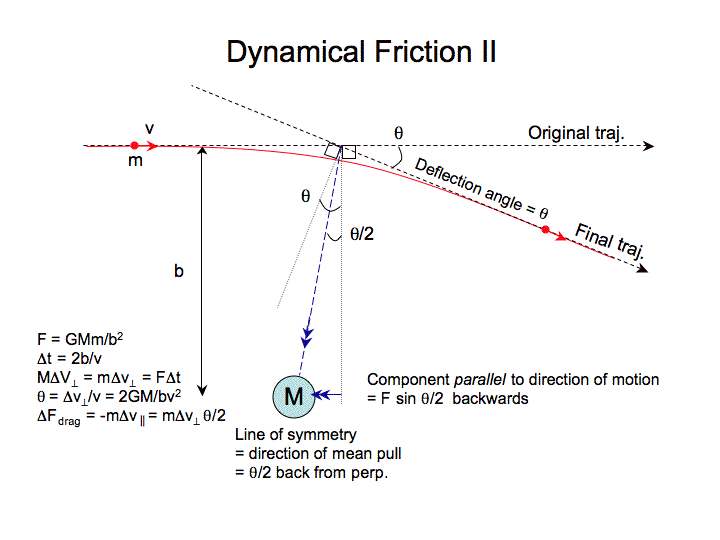
Method to evaluate the retarding force
The basic idea behind dynamical friction is that a moving mass attracts objects to it, but because of its motion, the objects tend to gather behind the mass, pulling it backwards.
To calculate the retarding force, it is best to think of a single object passing the mass on a Keplerian hyperbolic trajectory (i.e. jump to a frame moving with the mass). A simple analysis (see notes) approximates the full Keplerian solution. A small deflection angle 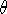 defines the direction of symmetry for the orbit which is tilted by
defines the direction of symmetry for the orbit which is tilted by 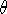 /2 to both incoming and outgoing asymptote. Thus, while momentum transfer occurs throughout the flyby, it can be approximated by the force at closest approach multiplied by the flyby time (roughly, 2b/v) in the direction of symmetry. Integrating over all encounters, the force perpendicular to the trajectory averages to zero, while the force parallel to it doesn't. You can follow the analysis using the notes and these figures.
/2 to both incoming and outgoing asymptote. Thus, while momentum transfer occurs throughout the flyby, it can be approximated by the force at closest approach multiplied by the flyby time (roughly, 2b/v) in the direction of symmetry. Integrating over all encounters, the force perpendicular to the trajectory averages to zero, while the force parallel to it doesn't. You can follow the analysis using the notes and these figures.
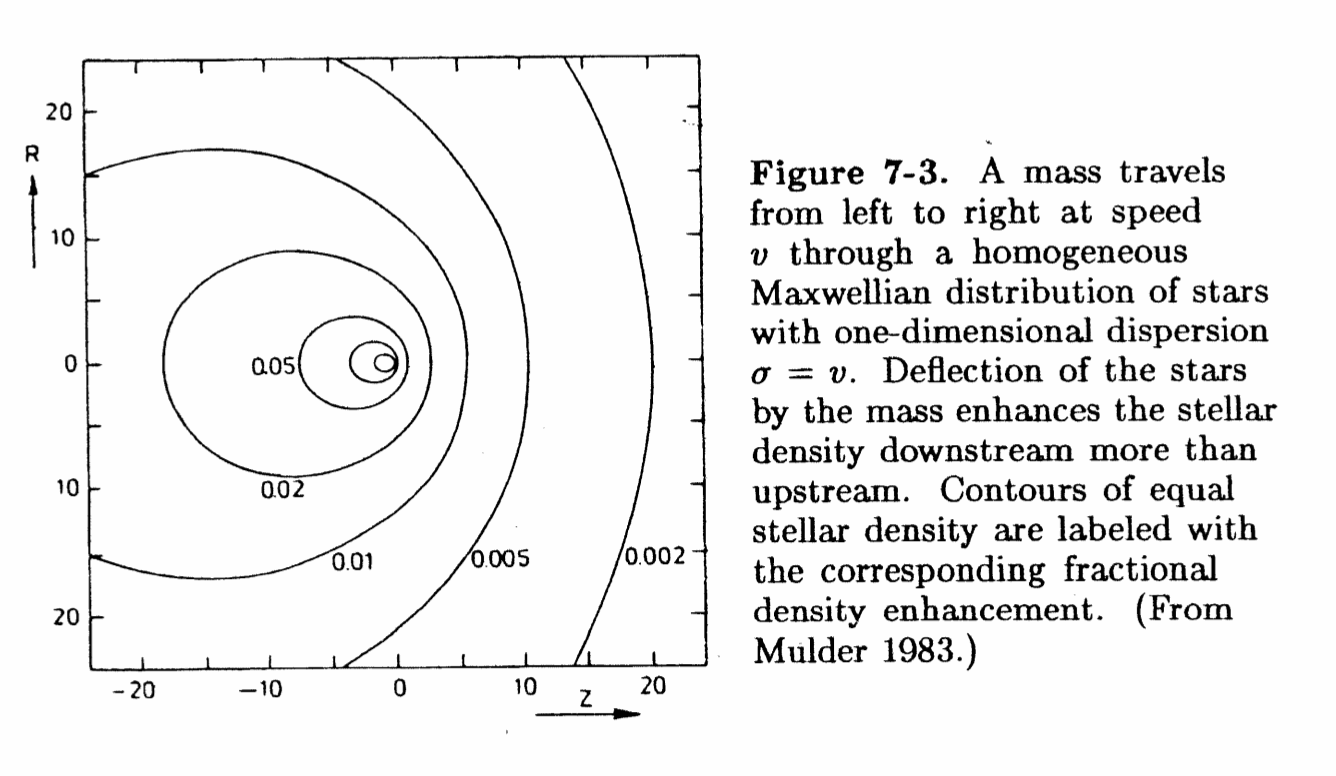
From B&T-I
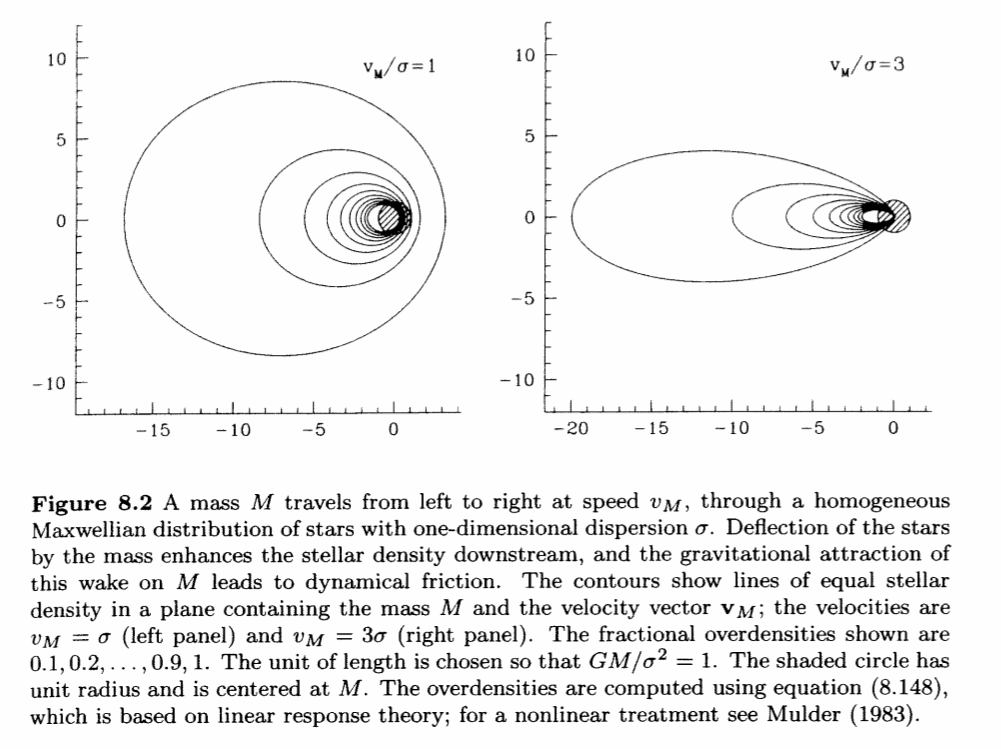
From B&T-II