Whittle: EXTRAGALACTIC ASTRONOMY




12. GALAXY INTERACTIONS & MERGERS


(1) Introduction
(a) Importance of Interactions
Our view of the importance of galaxy-galaxy interactions has changed
dramatically in the last 50 years.
- when galaxies were first discovered, they were termed "island universes"
they were thought of as isolated, fixed and essentially unchanging
- Hubble's classification scheme considered only normal undisturbed galaxies
only later were Irregular (type II) and peculiar classes added
Recognition of the importance of interactions gradually grew:
- Catalogs & surveys noted "peculiar" &/or closely paired galaxies
showing distortions and tails
- Since interactions are short lived (
 108yr),
their apparent rarity is misleading
108yr),
their apparent rarity is misleading
integrated over a Hubble time, many galaxies are expected to have experienced
interactions
- star formation was apparent in some systems
 deeper changes are occurring besides mere
morphological disturbance
deeper changes are occurring besides mere
morphological disturbance
- The difference in cluster and field Hubble type mix clearly
indicates that environment can affect morphology
Taken together, Galaxy-Galaxy interactions are important in
understanding many aspects galaxy evolution:
 Morphological and dynamical structures
Morphological and dynamical structures
 Star formation and starburst histories, with
associated chemical enrichment history
Star formation and starburst histories, with
associated chemical enrichment history
 AGN creation and fuelling
AGN creation and fuelling
 Elliptical galaxy formation
Elliptical galaxy formation
 Formation of all galaxies in the
Heirarchical merging scenario.
Formation of all galaxies in the
Heirarchical merging scenario.
(b) Different Physical Regimes
To help clarify this topic, keep in mind several different regimes: [e.g. image ]
- Strength of interaction:
- Weak and/or distant encounters:
flyby with associated tides
satellite orbit decay due to dynamical friction
tidal evaporation of orbiting satellite
tidal or gravitational shocks
- Strong and/or close encounters:
can lead to mergers
more global gravitational effects become important
- Relative size of merging galaxies:
major mergers: roughly equal sized galaxies
minor (eg satellite) mergers: one galaxy is significantly smaller than the other
- Hubble type of interacting/merging galaxies:
disks: dynamically cold (tend to generate narrow tidal tails)
spheroids: dynamically hot (tend to generate wider tidal fans)
- Different galaxy constituents:
these can respond quite differently during a merger and can play quite different
roles
stars: a collisionless system
gas: dissipational; star formation; feedback
dark matter: extended collisionless reservoire for absorbing Energy and AM
- Relics:
Visible effects can survive long after the main merger (or interaction)
has ended,
particularly at large radii where relaxation times are very long:
Polar rings
Shells
HI at large radii, possibly raining back down on the remnant
Kinematically distinct cores
Elliptical galaxies (may be merger relics!)



(2) Catalogs
(References below are taken from Bill Keel's web notes [o-link])
(a) Interactions
Recognising interactions/peculiarities is relatively easy
There are a number of catalogs, all derived from inspecting the PSS (or
equivalents):
- Vorontsov-Velyaminov 1959, Atlas and Catalog of Interacting Galaxies,
Shternberg Inst., Moscow; continued in 1972 A&ASuppl 28, 1.
- Arp 1966, Atlas of Peculiar Galaxies, Caltech; also appeared as ApJSuppl 14,1.
- Arp and Madore 1987, A Catalogue of Southern Peculiar Galaxies and Associations, Cambridge U.
- Johansson & Bergvall 1990 A&A Suppl 86, 167 (followup in A&A Suppl 113, 499, 1995)
selected pairs from the southern polar cap;
- Reduzzi and Rampazzo 1995 (ApL 30, 1) southern equivalent to northern Karachentsev pairs.
(b) Pairs
Once again  mergers/interactions may be important in the
history of all galaxies.
mergers/interactions may be important in the
history of all galaxies.



(3) Analytic Tools
We first consider four regimes which are analytically tractable as well as dynamically important.
They also develop our ability to interpret numerical simulations of more complex regimes.
(a) A small system moving through a larger one (dynamical friction)
(b) Tidally driven evaporation: the Jacobi (Roche) Limit
(c) "Slow" encounters, where Vinternal >>
 Vencounter (adiabatic approximation)
Vencounter (adiabatic approximation)
(d) "Fast" encounters, where Vinternal <<
 Vencounter (impulse approximation; tidal shocking)
Vencounter (impulse approximation; tidal shocking)
Unfortunately, major mergers do not conform to any of these regimes;
They cannot be treated analytically and require numerical simulation (see § 5)
(a) Dynamical Friction
- Consider a mass M moving at speed V through a population of stars
with uniform space density n.
The stars have mass m (<<M) velocity distribution f(v) (expressed as # per v) [image]
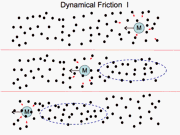
- Gravitational focussing creates a wake behind the moving mass which pulls back on it
This retarding force is called dynamical friction
(i) Simplified Derivation of the Retarding Force

- Consider a single star passing with impact parameter b
It experiences a force towards M of F
 GMm/b2 for a time
GMm/b2 for a time  t
t
 2b / V
2b / V
- After passing by, the impulse has imparted a perpendicular velocity:
- The (small) angle of deflection is therefore tan


 v
v / V =
2GM / bV2
/ V =
2GM / bV2
(this approximates the hyperbolic Kepler/Coulomb solution)
- The encounter has symmetry about the vector of closest approach
i.e. the line  /2 backwards from the original perpendicular impact parameter vector
/2 backwards from the original perpendicular impact parameter vector
Newton's 3rd law demands that the impulse felt by m is equal and opposite to
the impulse felt by M:
m v = M
v = M V
V
- We are interested in the component of the force parallel (and backwards) to the motion of M
(the perpendicular component will average to zero when summing over all stars)
So, we have for a single star's retarding impulse:
 I
I =
=  t
t  Fdrag =
-m
Fdrag =
-m v
v =
-m 2GM/bV tan
=
-m 2GM/bV tan 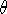 /2
= -2G2M2m / b2V3
/2
= -2G2M2m / b2V3
- Integrating over all impact parameters (2
 b db)
and over the encounter rate nV, we get:
b db)
and over the encounter rate nV, we get:
 |
(12.1) |
Here,  = bmax / bmin =
bmaxV2 / GM is the usual Coulomb logarithm
= bmax / bmin =
bmaxV2 / GM is the usual Coulomb logarithm
where bmin is defined when  v
v
 V and bmax is the effective size
of the region
V and bmax is the effective size
of the region
Note also that nm is simply the total density: 
- Approximately, we have for ln
 :
:
Open clusters ( 6); Globular Clusters (
6); Globular Clusters ( 11);
L* E galaxy (
11);
L* E galaxy ( 22);
Galaxy clusters (
22);
Galaxy clusters ( 7)
7)
- Allowing for an (isotropic) field star velocity distribution, f(v),
we get the
Chandrasekhar (1943) dynamical friction formula:
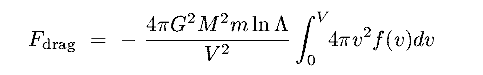 |
(12.2) |
Note the approximations used in this derivation:
M >> m the object significantly outweighs the field stars
M << Msystem the responding field distribution is
 symmetric
about the object
symmetric
about the object
the field stars have an isotropic velocity field
we have ignored the self gravity of the wake
Despite these approximations, the equation works well in a wide range
of situations.
(ii) Special Cases
- if M moves slowly compared to the stars: V << v:
we replace f(v) with f(0) to get:
Fdrag =
-(16/3) 2G2M2m ln
2G2M2m ln 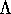 f(0) V
f(0) V
 only stationary stars contribute to the wake,
the rest quickly leave the area
only stationary stars contribute to the wake,
the rest quickly leave the area
 Since Fdrag
Since Fdrag  V, this resembles Stokes's law for motion through a viscous fluid.
V, this resembles Stokes's law for motion through a viscous fluid.
- if M moves fast compared to the stars: V >> v:
the integral converges, and we recover the simple equation 12.1
 all stars contribute to the wake
all stars contribute to the wake
 since with
Fdrag
since with
Fdrag  V-2,
the drag decreases for faster moving masses
V-2,
the drag decreases for faster moving masses
- for a Maxwellian f(v), with dispersion
 , we
obtain:
, we
obtain:
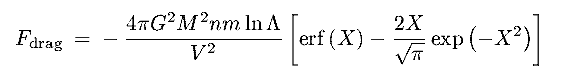 |
(12.3) |
where X = V / 
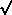 2 ( graph of [fcn] : 0 for X = 0 and 1.0 for X > 2.4)
2 ( graph of [fcn] : 0 for X = 0 and 1.0 for X > 2.4)
Note that the star masses enter as nm, ie the total mass density 
the drag is therefore independent of m, and the equation works for a spectrum of
masses
 Fdrag
Fdrag  M2 : gravitationally
focussed mass
M2 : gravitationally
focussed mass  M so force
M so force  M2
M2
 Fdrag
Fdrag  V-2 : fast objects
don't experience much drag.
V-2 : fast objects
don't experience much drag.
(iii) Applications of the Dynamical Friction Formula
- Satellite in Circular Orbit
For an isothermal galaxy with flat rotation curve Vc = const, we have:
 (r) = Vc2/ 4
(r) = Vc2/ 4 G
r2 ; dispersion
G
r2 ; dispersion
 = Vc/
= Vc/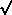 2 (ie X = 1);
giving Fdrag = -0.43 ln
2 (ie X = 1);
giving Fdrag = -0.43 ln 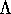 GM2/ r2
GM2/ r2
As the satellite spirals inwards, its angular momentum is always: L = MVcr
so, the rate of change of L is given by the torque:
dL/dt = Fdragr = -0.43 ln 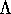 GM2/ r
GM2/ r
and we get
MVcr dr/dt = -0.43 ln 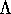 GM2
GM2
Solving this ODE from initial radius ri (at t=0) down to r=0 at tinfall, we get
½ ri2 = 0.43 ln 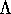 GM / Vc tinfall
GM / Vc tinfall
Using as fiducials, numbers appropriate for a Globular cluster orbiting the MW:
M = 106M ; Vc = 250 km/s;
bmax = ri = 2 kpc; (so ln
; Vc = 250 km/s;
bmax = ri = 2 kpc; (so ln 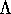
 10)
10)
This gives:
tinfall  2.6×1011
yr (ln
2.6×1011
yr (ln 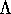 )-1 r2kpc2
V250 M6-1
)-1 r2kpc2
V250 M6-1
so although most GCs at large radii have not significantly changed their orbits,
GCs with initial radii r  1.5 kpc may have
already settled to the MW center.
1.5 kpc may have
already settled to the MW center.
- Massive Galaxy Encounter
Although this case is not strictly legitimate (M  Msystem)
it is nevertheless instructive:
Msystem)
it is nevertheless instructive:
for M  1010 M
1010 M ; ri
; ri  20 kpc; V
20 kpc; V  Vc
Vc
we get:
rinfall  2×108 yr
2×108 yr
 1 orbital period
1 orbital period
Clearly, massive galaxies entering each other's halos experience strong dynamical friction.
- Large and Small Magellanic Clouds
For the LMC, we have M  2×1010
M
2×1010
M and r
and r  60 kpc (so ln
60 kpc (so ln 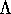
 3)
giving
3)
giving
tinfall  3×109 yr,
suggesting the LMC should have already spiralled inwards
3×109 yr,
suggesting the LMC should have already spiralled inwards
However: This assumes a circular orbit.
A more thorough analysis (Murai & Fujimoto '80) requires:
(a) that the LMC & SMC have remained bound to eachother in the past
(b) their orbital plane includes the HI Magellanic stream
[image]
They find: (B&T-I Fig 7.4 [image])
- the LMC+SMC orbit is elongated with pericenter/apocenter ratio
 0.5
0.5
- they are currently near pericenter
- their orbit has decayed by ×2 in radius over the past 1010yr
- the Magellanic stream came from the SMC following a close encounter with the LMC
2×108 yr ago
- the LMC and SMC will tidally separate when they come within 30 kpc of the
galaxy
- they will finally settle to the galactic center in further 1010 years.
(b) Tidally Driven Evaporation: Trunction and Disruption
-
The outer luminosity profiles of globular clusters are often sharply truncated
Naively, this is puzzling since stellar systems don't naturally have "edges"
-
The reason: outer stars become more bound to the galaxy than to the GC potential
This is an example of Tidal Stripping or Tidal Truncation [image]
(Similar effects are seen in some cluster galaxies)
(i) Tidal (Jacobi/Roche) Limit
-
How far must a star "wander" from its satellite before it is lost to the galaxy ?
If you answer: "where the r-2 force of the satellite and galaxy are
balanced" you would be wrong
You forgot to include the fact that the satellite
is also orbiting the galaxy
The satellite and galaxy are "fixed" only in a rotating frame, in
which pseudo-forces are also important.
-
In this rotating frame, the star's energy E = ½V2 +
 (r) is not conserved
(r) is not conserved
(recall, space probes can use planets to gain energy in a "gravitational slingshot")
Instead, the Jacobi Integral EJ = ½V2 +
 eff(r) is conserved;
eff(r) is conserved;
where we have again introduced the effective potential in a rotating frame:
 eff(r) =
eff(r) =
 (r) - ½
|
(r) - ½
|  × r |2
× r |2
where  refers to the satellite's orbit
and r has origin at the Center of Gravity (
refers to the satellite's orbit
and r has origin at the Center of Gravity ( galaxy center)
galaxy center)
Here is a contour plot of  eff(r) for two point masses:
[images]
eff(r) for two point masses:
[images]
-
Note the 5 Lagrange points: maxima in
 eff
where stars are stationary (in the rotating frame)
eff
where stars are stationary (in the rotating frame)
L1 is the deepest; L1, L2, L3 are unstable; L4, L5 are stable
(recall, Trojan asteroids)
(although L4, L5 are maxima, coriolis force keeps objects in a slow "epicyclic
orbit" around them)
-
Consider the simplest case:
two point masses: a small satellite in circular orbit about a massive galaxy (ie m<<M)
evaluate  eff along a line connecting
m and M (separation R), with origin at m: [example]
eff along a line connecting
m and M (separation R), with origin at m: [example]
 eff(x) = - GM / |R - x| -
Gm / |x| - ½
eff(x) = - GM / |R - x| -
Gm / |x| - ½  2(x - R)2
2(x - R)2
Now find the turning points :
substitute for  2 = GM / R3;
differentiate w.r.t. x;
set to zero and solve for x = rJ:
2 = GM / R3;
differentiate w.r.t. x;
set to zero and solve for x = rJ:
rJ = R(m / 3M)1/3 is the Jacobi Limit (also
called the tidal or Roche radius, or Hill radius)
-
If we re-calculate for the case of a galaxy with isothermal (flat Vrot) galaxy halo, we get:
In general, a useful approximation is that rJ marks the point at which:
the orbital period of the satellite about the galaxy is similar to
the orbital period of a star about the satellite (in the absence of the galaxy).
-
In practice, measured tidal radii agree only roughly with our simple expression for rJ.
The derivation should be considered as indicative rather than predictive.
(ii) Satellite Evaporation and Possible Destruction
-
The value of
 eff at rJ divides
stars into those which can escape from those which cannot
eff at rJ divides
stars into those which can escape from those which cannot
Consider a satellite star with EJ moving away from the satellite: V is decreasing
as the star approaches the contour  eff =
EJ, V approaches zero and the star turns around
eff =
EJ, V approaches zero and the star turns around
Clearly, if EJ >  eff(rJ)
then the star crosses the critical contour
eff(rJ)
then the star crosses the critical contour
If this happens to be near L1 (or L2), the star proceeds "down hill"
and is lost from the satellite
Thus, over time we expect to lose all stars with EJ >
 eff(rJ)
eff(rJ)
-
The satellite evaporates, in the sense that it is losing stars with the highest energy
Unlike the slow evaporation of an isolated cluster, when stars scatter into orbits
with V > Vesc (see Topic 8.10.d.iii),
tidal evaporation is independent of scattering within the cluster:
 even bound stars
(ie E < 0 for an isolated satellite) can have EJ >
even bound stars
(ie E < 0 for an isolated satellite) can have EJ >
 eff(rJ) and can be lost
eff(rJ) and can be lost
-
For a satellite which is approaching a galaxy, rJ and
 eff(rJ) continually decrease:
eff(rJ) continually decrease:
 the cluster may lose an ever increasing number of stars.
the cluster may lose an ever increasing number of stars.
Recall from Topic 8.7.e that most stars are marginally bound
(ie N(E) peaks near
E  0 ):
0 ):
 a small decrease in
a small decrease in  eff(rJ) can
result in the loss of many stars.
eff(rJ) can
result in the loss of many stars.
-
Nice example of tidal evaporation in a MW globular cluster Palomar 5: [images]
Here's a simulation of the tidal destruction of a dwarf satellite by Kathryn Johnston: [movie]
(c) Adiabatic Approximation (Slow Encounter)
-
During a tidal encounter, the orbits of many stars are significantly
affected.
However, some orbits are not greatly affected: those for which
torbit << tencounter
As the tidal field slowly changes, the orbit responds slowly and
reversibly
 cf the response of the moon's orbit during
the year as the Earth's distance to the sun changes
cf the response of the moon's orbit during
the year as the Earth's distance to the sun changes
This type of response is called adiabatic
-
If the encounter is a "flyby", the tidal field first grows, then decays
 the rapid
orbits slowly modify, but then return to their original form
the rapid
orbits slowly modify, but then return to their original form
Thus, stars on rapid orbits near galaxy centers are not greatly affected
by tidal encounters
(unless, of course, the encounter proceeds to become a merger)
(d) Impulse Approximation (Fast Encounter: Tidal Shocks)
- The opposite extreme occurs when torbit >>
tencounter
This occurs when Vinternal <<  Vencounter
Vencounter
In this case stars don't move much during the encounter
 no change in PE :
no change in PE :  PE
PE
 0
0
However, they do feel an impulse, (ie a force acting over a short time)
 changes in both global and
internal velocities:
changes in both global and
internal velocities:
 VCM and
VCM and
 Vinternal (B&T p434-435)
Vinternal (B&T p434-435)
 so internal KE does change:
so internal KE does change:
 KE
KE  ½
½
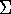 m
m  Vint2
(note: always +ve)
Vint2
(note: always +ve)
 The effect of the tidal shock is
to heat the stars
The effect of the tidal shock is
to heat the stars
We say the system has experienced a tidal shock
-
How does the system respond (relax) after experiencing the tidal shock ?
Loosely speaking:
the increased KE causes the system to expand and cool
(recall, self gravitating star systems have -ve specific heat: Topic 8.5e and [image])
More formally:
using subscripts o="original", i="initially after encounter",
and f="finally after relaxation"
Virial theorem applies to the original and final relaxed systems:
Eo = -KEo and Ef = -KEf (see Topic 8.5)
immediately following the encounter we have: KEi = KEo +
 KE and Ei = Eo +
KE and Ei = Eo +  KE
= -KEo +
KE
= -KEo +
 KE
KE
following relaxation, we have: Ef = Ei
 -KEf = -KEo +
-KEf = -KEo +
 KE giving KEf = KEo -
KE giving KEf = KEo -
 KE
KE
 from original to final, the system has
indeed cooled, by
an amount
from original to final, the system has
indeed cooled, by
an amount  KE
KE
 since the shock heats the original
system by
since the shock heats the original
system by  KE, then
KE, then
during relaxation (i to f) the system cools by -2 KE
(ie KEf = KEi - 2
KE
(ie KEf = KEi - 2 KE)
KE)
of course, the system has also expanded, increasing the final PE by
 KE
KE
-
Since the stars receive energy, some may become unbound (E > 0)
 these are lost from the system: they evaporate
these are lost from the system: they evaporate
If there are repeated tidal shocks, a cluster may be disrupted and disintegrate
- Finally, if the encounter is distant, the "tidal approximation" applies:
(B&T-I p 437-438)
eg, a spherical system (mass M, rms size r) is passed by a mass m at distance
b with speed V
 the change in its energy is
the change in its energy is
 E
E  (4 G2M2m r2) / (3 b3V4)
(4 G2M2m r2) / (3 b3V4)
 it is left elongated, long axis pointing
to the point of closest approach (cf lunar tides)
it is left elongated, long axis pointing
to the point of closest approach (cf lunar tides)
-
Examples:
- Open clusters are shocked by the passage of Dense Molecular Clouds (DMCs)
 there are very few old open clusters
there are very few old open clusters
 most
have evaporated from repeated shocks on a timescale
most
have evaporated from repeated shocks on a timescale  5×108 yr.
5×108 yr.
- Globular Clusters are shocked when they pass through the MW disk
 can lead to evaporative disruption (depends
on where in the disk )
can lead to evaporative disruption (depends
on where in the disk )
eg for GC with  =
5 km/s, r = 10pc, V
=
5 km/s, r = 10pc, V = 170 km/s crossing at
at
= 170 km/s crossing at
at  3.5 kpc,
3.5 kpc,
 disruption timescale is
disruption timescale is
 6×109 yr
6×109 yr
- Tidal shocking of galaxies in clusters is termed: galaxy harassment
 disks are heated
disks are heated  they get thicker and
Toomre's Q parameter increases (see Topic 6.5a)
they get thicker and
Toomre's Q parameter increases (see Topic 6.5a)
 spiral arm formation is therefore
suppressed
spiral arm formation is therefore
suppressed
 appear to have earlier Hubble types (eg Sb
appear to have earlier Hubble types (eg Sb  Sa)
Sa)
Also, stars and dark matter expand and are lost to the galaxy but join the cluster
Gas, however, loses AM and goes to the center to trigger a starburst (see also sec 5c iii
This movie shows these processes in action: [movie]
- Ring galaxies are formed from tidal shocks [examples]
Perturber passes rapidly through & close to center of a disk galaxy (V >> Vc)
 shock induces
shock induces  Vr
Vr

 Vc(Vc /
V) radially inwards for all stars
Vc(Vc /
V) radially inwards for all stars
 this sets up synchronised
epicyclic motion
this sets up synchronised
epicyclic motion
(recall, velocity perturbations to orbiting stars yield epicyclic motion;
see 8.2)
the response is an expanding circular density wave
 a ring !
a ring !
these density waves can, of course, trigger star formation
The most famous is the "cartwheel": [images]
- Many shocks occur within the assembly of a rich cluster: [movie - 17Mb]
Fast close passages result in the ejection of many stars into the general cluster volume.
This movie/simulation is by John Dubinsky, with sound composed by John Farah.



(4) Numerical Simulations: Methods



(5) Numerical Simulations: Results
Simulations have been applied in a range of circumstances
(a) Flyby and Tidal Tails
(b) Minor Mergers and Satellite Accretion
(c) Major Mergers
- Here are two scenarios:
Roughly equal mass mergers: [image & movie].
Compact group mergers: [image & movie].
A page from Josh Barnes website has several movies that accompany this 1992 and 1996 papers: [o-link]
A page from Chris Mihos website also has several movies[o-link]
From these and many other simulations, a number of general results have emerged:
(i) Global Behaviour
- Mergers are surprisingly rapid : 1 - few orbital times.
Galaxy components settle on 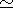 dynamical timescale
dynamical timescale
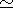 1 /
1 / 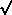 (G <
(G < >)
>)
as < > increases, settling speeds up: [movie 0.4Mb] by Josh Barnes and [image]
> increases, settling speeds up: [movie 0.4Mb] by Josh Barnes and [image]
 first couple of passes take a while
first couple of passes take a while
 third & fourth are much quicker
third & fourth are much quicker
 final merging happens rapidly
final merging happens rapidly
Large scale inhomogeneities cause globally acting torques
Angular momentum transfer is much faster than the idealized dynamical friction formula
- Galaxy encounters are very sticky
Even hyperbolic encounters can result in capture and merger (B&T-I Fig 7.9 [image])
This is mainly because the AM and Energy of the orbit is transferred to internal motions
(particularly the halo -- see next)
- Dark Matter halos play a crucial role in the merger [image]
Here's why:
- it is the Dark Matter halo which absorbs most of the orbital AM and energy
this occurs via:
 strong dynamical friction
strong dynamical friction
 global torques acting across the complex mass distribution.
global torques acting across the complex mass distribution.
(note that tidal tails only exert a modest torque on the galaxies)
- at a simpler level, even if stellar systems "miss" eachother, the DM halos
will "collide"
 ie the halos significantly increase the cross-section for interactions/mergers
ie the halos significantly increase the cross-section for interactions/mergers
In summary:
Without DM halos, galaxies would only slowly spiral inwards and mergers
would be rare
- As with flybys, the spin-orbit alignment can affect the merger timescale
prograde encounters lead to quicker merging than retrograde encounters
(ii) Behaviour of Stars (Collisionless Components)
- Disks are fragile, they are destroyed during the merger [movie-1 6.4Mb] and [image] and [movie-2 0.4Mb]
Bulges merge at the center
Violent relaxation occurs, but is incomplete
 significant phase space structure remains
significant phase space structure remains
 even though the actual space density is smooth [image]
even though the actual space density is smooth [image]
- The final density distribution is close to an R¼ law
this is due to:
 R¼ law components present
in the progenitors,
R¼ law components present
in the progenitors,
 the dynamical effects of the merger.
the dynamical effects of the merger.
The classic demonstration of this was for NGC 7252 (Schweizer 1982,
[images])
 Formation mechanism for at least some ellipticals: [image]
Formation mechanism for at least some ellipticals: [image]
- For a "head on" collision (ie b
 0)
the final product tends to be prolate or triaxial with little rotation
0)
the final product tends to be prolate or triaxial with little rotation
For an oblique collision (b significant) the end product tends to be
axisymmetric with some rotation.
(iii) Behaviour of Gas (Dissipational Component)
- Gas follows much of the general behaviour described in (i) above
However, it behaves quite differently from the collisionless component described in (ii) above
Stated simply: [image] (From Josh Barnes).
some gas is heated and leaves the system
some gas can cool and goes to the center.
- Let's focus on the gas going to the center:
Clearly, the gas is losing its angular momentum, but how does this happen?
The response of both the stars and gas to the first passage is to form a strong
bar [images]
However, the gas is shocked on the leading edge of the bar
This leads to an angular offset of the gas and star bars
The gravitational pull on the gas by the stars drains angular
momentum from the gas
The gas now falls towards the center and forms a small nuclear disk
This process is remarkably efficient:
 99% of the gas AM can be lost.
99% of the gas AM can be lost.
- When the two galaxies finally merge, the two nuclear gas disks also merge: [images and movies]
-
The inflow of gas also depends critically on its radiative cooling
Simulations without cooling have little gas going to the center [image]
The reason is that dissipational settling necessarily releases energy (virial
theorem!).
Without cooling the gas either escapes as a hot wind or is supported
by thermal pressure.
(iv) Fueling Starbursts and AGN
- As gas goes to the center [image], we expect high nuclear
star formation rates
 Starburst
Starburst
The simulations confirm this, showing large spikes in the SFR [image]
This is a major success: showing how starbursts/LIGs/ULIGS can arise from mergers
Future modelling will try to get the physics more accurate:
 aiming to reproduce
aspects such as superwinds, chemical enrichment, and ISM energetics.
aiming to reproduce
aspects such as superwinds, chemical enrichment, and ISM energetics.
- There is considerable evidence that interactions fuel AGN activity [images]
While is seems plausible that some gas reaches a central black hole, there is a gigantic AM barrier:
Need to take 200 km/s gas at 1 kpc down to 104 km/s at 10-4 pc (BH accretion disk)
This requires a loss in AM by a factor  105
105
The merger might get a factor 102 but that leaves another factor of 1000 !
Recent simulations follow the inner regions with ever-finer resolution [o-link]
It seems that gas can indeed get all the way down to feed a black hole.
(v) Future Collision between Milky Way and M31
- The Milky Way and M31 are currently approaching at 120 km/s and will merge in 3-4 Gyr
The details of the merger aren't known, since no proper motion is yet measured for M31
There have been a number of attempts to model this encounter: here's one by John Dubinsky: [images]



(6) Merger Relics
Although ongoing mergers are quite rare (they are short lived),
former mergers (relics) should be common
There are a number of possible examples, though we start with a
rather special one.
(a) Elliptical Galaxy Formation
- The possibility of mergers becoming ellipticals was suggested in '77 by Toomre [image]
Here was his reasoning:
-
Violent relaxation scrambles disks to yield a smooth and dynamically hot system (= elliptical?)
-
Statistically: we see
 10 local mergers, which each
last
10 local mergers, which each
last  8×108 yr
8×108 yr
Allowing for cosmic expansion, we expect an encounter rate  t5/3
t5/3
 expect
expect  750
ellipticals locally, which is about correct
750
ellipticals locally, which is about correct
- If merger endpoints are not ellipticals, then what are they ??
-
A bit later, Schweizer ('82) studied the merger NGC 7252 [images]
- It has an approximate R1/4 brightness profile spanning 7 magnitudes
- The central light profile keeps rising with PL index
 -1.3
-1.3
- It has a high central surface brightness and luminosity density
- Its core properties fit the 2-parameter correlations for Spheroids
These are all properties associated with Ellipticals (not all were measured in '82)
- The suggestion that Ellipticals were merger remnants has an interesting history
The idea met with considerable (unreasonable?) resistance
Here are some of the objections, with their (current) responses:
- Elliptical phase space density is higher than spirals,
but violent relaxation preserves phase space density.
Answer: gas dissipation and star formation can increase the phase space
density
- Ellipticals have many more globular clusters (per unit luminosity) than spirals
Answer: globular clusters are formed during mergers
- Ellipticals are found in clusters, where
 V is too
large for mergers
V is too
large for mergers
Answer: Clusters form heirarchically; Ellipticals form earlier in
smaller groups
- How can merging spirals preserve/create the metallicity - luminosity/radius
correlations ?
Answer: star formation during the merger liberates metals
-
The question of whether all Ellipticals formed by spiral mergers is still open
However, in the heirarchical picture all galaxies formed by merger, the question now becomes:
 what merged to form Ellipticals?
what merged to form Ellipticals?
High-z observations show some cluster ellipticals formed early, before massive spiral disks
Maybe Cluster and Field ellipticals have different origins?
One possibility:
- Cluster Ellipticals form from the rapid assembly of many smaller progenitors
- Field Ellipticals form from the merger of spirals
This must remain speculative, not least because cluster and field ellipticals are
observationally almost indistinguishable
(b) Counter-Rotating Disks
- Recall that in mergers, the gas can experience 99% loss of AM
In such a chaotic process, the final AM of the most nuclear gas may be quite unrelated to the initial AM.
Nice examples of this can be found both in simulations and in real galaxies: [images]
Their merger remnant contained a counter-rotating nuclear gas disk
- If star formation ensues, a counter-rotating stellar disk will result
Of course, counter-rotation is only the most dramatic endpoint.
In general one may form a "Kinematically Distinct Core" (KDC)
Such systems are seen in a significant fraction ( 25%)
of ellipticals (see Topic 7.6d)
25%)
of ellipticals (see Topic 7.6d)
- KDCs can also form in minor mergers when a gas rich spiral falls into a pre-existing elliptical:
[image].
(c) Polar Ring Galaxies
-
Polar ring galaxies are quite rare and are thought to arise from accretion
They usually comprise an S0 galaxy with approximately  r ring of material (gas &/or stars)
r ring of material (gas &/or stars)
Archetype is NGC 4650A, though there are other nice examples [images]
(Note: these are not to be confused with ring galaxies which have rings in galaxies)
- Usually, an accreted companion ends up in the primary's disk
Occasionally, however, gas enters an approximately polar orbit
Although most inclined orbits are unstable, those close to a  r plane can be stable
r plane can be stable
- Star formation in the ring can then lead to a stellar component
Age estimates of a few Gyr confirm that polar rings are quite stable.
- If accretion angles are random, then only
 few % will find stable polar orbits
few % will find stable polar orbits
 much larger fraction of S0s experience accretion (at the other angles)
much larger fraction of S0s experience accretion (at the other angles)
(d) Shell Galaxies






 108yr),
their apparent rarity is misleading
108yr),
their apparent rarity is misleading  deeper changes are occurring besides mere
morphological disturbance
deeper changes are occurring besides mere
morphological disturbance  Vencounter (adiabatic approximation)
Vencounter (adiabatic approximation)


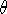
 =
=  b db)
and over the encounter rate nV, we get:
b db)
and over the encounter rate nV, we get:
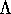 = bmax / bmin =
bmaxV2 / GM is the usual Coulomb logarithm
= bmax / bmin =
bmaxV2 / GM is the usual Coulomb logarithm 
 V, this resembles Stokes's law for motion through a viscous fluid.
V, this resembles Stokes's law for motion through a viscous fluid.
 , we
obtain:
, we
obtain:
 2 (
2 ( ; Vc = 250 km/s;
bmax = ri = 2 kpc; (so ln
; Vc = 250 km/s;
bmax = ri = 2 kpc; (so ln  1.5 kpc may have
already settled to the MW center.
1.5 kpc may have
already settled to the MW center.
 (r) is not conserved
(r) is not conserved  × r |2
× r |2
 m
m 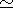 104-5 M
104-5 M with
with