We have reverted to the familiar notion of gravity, away from the more correct concept of warped spacetime, because speaking in terms of gravity makes our discussion of the evolution of the universe much easier to understand. However, general relativity makes some predictions that do not have a simple description in Newtonian terms. Foremost among these is the fact that space is curved, with the degree of curvature determined by the amount of matter within it. The curvature must be the same everywhere (because of the cosmological principle), so there are only three distinct possibilities for the large-scale geometry of the universe, and they correspond to the possible futures we have just described. For more information on the different types of geometry involved, see More Precisely 26-1.

If the average density of the cosmos is above the critical value, space is curved so much that it bends back on itself and "closes off," making this bound universe finite in size. Such a universe is known as a closed universe. It is difficult to visualize a three-dimensional volume uniformly arching back on itself in this way, but the two-dimensional version is well known: it is just the surface of a sphere, as with the balloon we discussed earlier. Figure 26.5, then, is the two-dimensional likeness of a three-dimensional closed universe. Like the surface of a sphere, a closed universe has no boundary, yet it is finite in extent. (Notice that for the sphere analogy to work, we must imagine ourselves as two-dimensional "flatlanders" who cannot visualize or experience in any way the third dimension perpendicular to the sphere's surface. Flatlanders are confined to the sphere's surface, just as we are confined to the three-dimensional volume of our universe.) One remarkable property of a closed universe is illustrated in Figure 26.13. Just as a traveler on the surface of a sphere can keep moving forward in a straight line and eventually return to her starting point, a flashlight beam shone in some direction in space might eventually traverse the entire universe and return from the opposite direction!

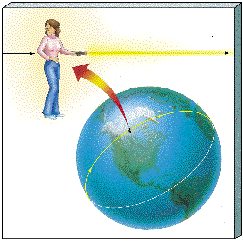
Figure 26.13 In a closed universe a beam of light launched in one direction may return someday from the opposite direction after circling the universe, just as motion in a "straight line" on Earth's surface will eventually encircle the globe.

The surface of a sphere curves, loosely speaking, "in the same direction" no matter which way we move from a given point. A sphere is said to have positive curvature. However, if the average density of the universe is below the critical value, the surface curves like a saddle. It has negative curvature. Most people have a good idea of what a saddle looks like---it curves "up" in one direction and "down" in another, but no one has ever seen a uniformly negatively curved surface, for the simple reason that it cannot be constructed in three-dimensional Euclidean space! It is just "too big" to fit. A low-density, unbound, saddle-curved universe is infinite in extent and is usually called an open universe.

The intermediate case, in which the density is precisely equal to the critical density, is the easiest to visualize. This universe, called a critical universe, has no curvature. It is said to be "flat," and it is infinite in extent. In this case, and only in this case, the geometry of space on large scales is precisely the familiar Euclidean geometry taught in high schools. Apart from its overall expansion, this is basically the universe that Newton knew.

Euclidean geometry---the geometry of flat space---is familiar to most of us because it is a good description of space in the vicinity of Earth. It is the geometry of everyday experience. Does this mean that the universe is flat, which would in turn mean that it has exactly the critical density? The answer is no. Just as a flat street map is a good representation of a city, even though we know Earth is really a sphere, Euclidean geometry is a good description of space within the solar system, or even the Galaxy, because the curvature of the universe is negligible on scales smaller than about 1000 Mpc. Only on the very largest scales do the geometric effects we have just discussed become evident.