Is there any way for us to determine which of these models actually describes our universe (that is, apart from just waiting to find out)? Will the universe end as a small, dense point much like that from which it began? Or will it expand forever? Fortunately, we live at a time when astronomers are subjecting these questions to observational tests. Unfortunately, the results of these observations are still inconclusive.
The most straightforward approach is to try to estimate the universe's average density, because density is the basic quantity that distinguishes one model from the other. As just noted, for H0 = 65 km/s/Mpc, the critical density that separates the two possible futures is about 10-26 kg/m3. Cosmologists conventionally call the ratio of the actual density to the critical value the cosmic density parameter and denote it by the symbol ("omega nought"). In terms of this quantity, then, a critical universe has
= 1. A universe with
less than 1 will expand forever; one with
greater than 1 will recollapse.
How can we determine the average density of the universe? On the face of it, it would seem simple—just measure the average mass of the galaxies residing within some large parcel of space, calculate the volume of that space, and compute the total mass density. When astronomers do this, they usually find a little less than 10-28 kg/m3 in the form of luminous matter. Largely independent of whether the chosen region contains many scattered galaxies or only a few rich galaxy clusters, the resulting density is about the same, within a factor of 2 or 3. Galaxy counts thus yield to be about 0.01. If that measure were correct, then the universe would expand forever.
But there is an important additional consideration. We have noted (Chapters 23 and 24) that most of the matter in the universe is dark—it exists in the form of invisible material that has been detected only through its gravitational effect in galaxies and galaxy clusters.
(Secs. 23.6, 24.3) We currently do not know what the dark matter is, but we do know that it is there. Galaxies may contain as much as 10 times more dark matter than luminous material, and the figure for galaxy clusters is even higher—perhaps as much as 95 percent of the total mass in clusters is invisible. Even though we cannot see it, dark matter contributes to the average density of the universe and plays its part in opposing the expansion. Including all the dark matter that is known to exist in galaxies and galaxy clusters increases the value of
to 0.2 or 0.3—still less than 1, implying an unbound universe, but a lot closer to 1 than the 0.01 value calculated using visible matter only.
Unfortunately, the distribution of dark matter on larger scales is not very well known. We can infer its presence in galaxies and galaxy clusters, but we are largely ignorant of its extent in superclusters, voids, or other larger structures. However, there are indications that it accounts for an even greater fraction of the mass on large scales than it does in galaxy clusters. For example, observations of gravitational lensing by galaxy clusters suggest that dark matter may be even more extensive than is indicated by the motion of galaxies within the clusters. (Sec. 25.5) Furthermore, optical and infrared observations of the overall motion of galaxies in the local supercluster suggest the presence of a nearby huge accumulation of mass known as the Great Attractor, with a total mass of about 1017 solar masses and a size of 100—150 Mpc. If the current best estimates of the size and mass of this gargantuan object are correct, its average density may be quite close to the critical value.
Thus it is quite conceivable that invisible matter may account for as much as 99 percent of the total mass in the universe. In that case, the vast "voids" are not empty at all—they are huge seas of invisible matter, and the visible galaxies are merely insignificant "islands" of brightness within them. If the total amount of dark matter lurking in the darkness beyond the galaxy clusters exceeds the luminous mass by a factor of 100 or more, may even exceed 1, and the universe will recollapse. This is why it is so important to search for reservoirs of invisible matter beyond the galaxies. The measured value of
has steadily increased over the past 20 years as larger and larger regions of the universe have been surveyed.
Determining the mass density of the universe is an example of a local measurement that provides an estimate of . But the result we obtain depends on just how local our measurement is—the larger the scale, the larger the result we obtain. In an attempt to get around this problem, astronomers have devised alternative methods that rely instead on global measurements, which cover a much larger portion of the observable universe. The idea is that global tests should indicate the universe's overall density, not just its value in our vicinity.
One such global method attempts to measure the deceleration of the universe directly by observing faraway galaxies. The universe expanded faster in the past, and the greater the average density of the universe, the greater the deceleration has been. The issue facing astronomers is to determine the rate at which the expansion is slowing, because this translates directly into an estimate of the density.
Astronomers cannot hope to measure the cosmic slowdown by watching the motion of any one galaxy. But because the expansion is slowing, objects at great distances—that is, objects that emitted their radiation long ago—should appear to be receding faster than Hubble's law predicts. Figure 26.11 illustrates this concept. If the universal expansion were constant in time, recessional velocity and distance would be related by a straight line—the solid line in the figure. However, in a decelerating universe, the recessional velocity is greater at large distances (that is, at times in the distant past). This velocity difference is greater for a denser universe, in which gravity has been more effective at slowing the initial expansion.
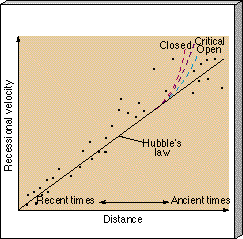
Figure 26.11 An idealized diagram showing how we might detect evidence for a deceleration of the universe by observing a departure from Hubble's law (solid line). The dashed curves show the expected departure for different evolving models of the universe (exaggerated for clarity.)
As indicated in the figure, many distant galaxies do seem to have recessional velocities substantially greater than Hubble's law would predict. Unfortunately, these galaxies are generally very faint and accurate measurements of their properties are difficult. The uncertainties in their measured distances (which are much greater than the uncertainties in the velocities) mean that we currently cannot distinguish among the various models based on these observations.
In 1998, astronomers announced the first results from a long-term, systematic survey of distant Type-I (carbon-detonation) supernovae. (Sec. 21.3) Recall from Section 24.2 that Type-I supernovae have a remarkably narrow spread in luminosities, making them particularly useful as distance-measurement tools. Far from clarifying the picture of cosmic deceleration, however, these findings seem to indicate that the expansion of the universe is not slowing, but actually accelerating! According to the supernova data, galaxies at large distances are receding less rapidly than Hubble's law would predict. These observations, if confirmed, are inconsistent with the standard Big Bang model presented in this chapter, and may precessitate a major revision of our view of the cosmos. Interlude 27-1 discusses one possible interpretation of these results.
So, what is the ultimate fate of the universe? The answer is still not known with absolute assurance. However, although there is a large uncertainty in the value of , most astronomers would probably agree that it lies between 0.1 and 1. As best we can tell, given the current data, the universe is destined to expand forever.
In Section 26.2, when we estimated the age of the universe from the accepted value of Hubble's constant, we made the assumption that the expansion speeds of the galaxies were constant in the past. However, as we have now found, this is not the case. At least within the Standard Big Bang model, the effects of gravity have slowed the universe's expansion over time, so, regardless of which evolutionary model turns out to be correct, the universe must have expanded faster in the past than it does today. The assumption of a constant expansion rate therefore leads to an overestimate of the universe's age—the universe is actually younger than the 15 billion years we calculated earlier. How much younger depends on how much deceleration has occurred.
Figure 26.12 illustrates this point. It is similar to Figure 26.9, except that here we have added a line corresponding to constant expansion at the present rate—a completely empty universe that is 15 billion years old. Because all the models we have discussed lie below this line, we can see graphically that the true age of the universe is indeed less than the age obtained assuming a constant expansion speed. In the special case of critical density, the age of the universe happens to be particularly easy to calculate—it is two-thirds of the foregoing value, or 10 billion years. (This was the assumption underlying Table 25.1 in More Precisely 25-1.) A low-density, unbound universe is older than 10 billion years (but still less than 15 billion years old); a high-density, bound universe is younger.
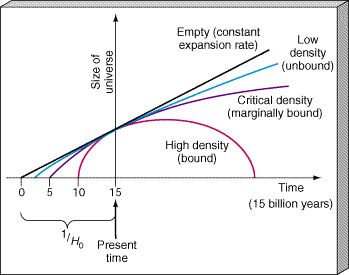
Figure 26.12 As the density of the universe increases, its deceleration increases, too. The universe contains some matter, so whatever the model, its trajectory on this graph will lie below the line for the constant-expansion-rate empty universe. Thus, the age of the universe is always less than 1/H0. The true age decreases for larger values of the present density.
Impressive though it is that we can pin down the age of the universe to within less than a factor of 2, these numbers highlight a continuing problem in astronomy. Unless the universe is of quite low density, and hence closer to 15 billion years old, the age that we obtain from cosmology is uncomfortably close to the low end of the 10—12-billion-year age range implied by studies of globular clusters in our own Galaxy (see Chapters 17 and 20).
(Secs. 17.10, 20.5) Because the Galaxy cannot be older than the universe, and because the density of the universe appears to be at least relatively close to the critical value (see also Section 27.4), we are forced to conclude that there may be a contradiction between these two major areas of astronomy.
If, as observations improve, Hubble's constant turns out to be closer to 50 or 60 km/s/Mpc, and if the upper limit on globular-cluster ages can be reduced, then the two age estimates may be reconciled. However, if Hubble's constant is more like 70 or 80 km/s/Mpc, then the discrepancy may become a serious embarrassment to astronomy. Interlude 26-2 explores this topic in a little more detail.