In the late 1970s, cosmologists trying to piece together the evolution of the universe were confronted with two nagging problems that had no easy explanation within the standard Big Bang model. The resolution of these difficulties caused cosmologists to rethink their view of the very early universe.
The first problem is known as the horizon problem, and it concerns the remarkable isotropy of the cosmic microwave background. Recall that the temperature of this radiation is virtually constant, at about 2.7 K, in all directions. Imagine observing the microwave background in two opposite directions on the sky, as illustrated in Figure 27.8. As we have just seen, the radiation last interacted with matter in the universe around a redshift of 1500. Thus, in observing these two distant regions of the universe, marked A and B on the figure, we are studying regions that were separated by several million parsecs at the time that they emitted this radiation. The fact that the background radiation is isotropic to high accuracy means that regions A and B had very similar densities and temperatures at the time the radiation we see left them. The problem is, within the Big Bang theory as just described, there is no particular reason why these regions should be so similar to each other.

Figure 27.8 The horizon problem. The isotropy of the microwave background indicates that regions A and B in the universe were very similar to each other when the radiation we observe left them, but there has not been enough time since the Big Bang for them ever to have interacted physically with one another. Why then should they look the same?
To take an everyday example, we all know that heat flows from regions of high temperature to regions of low temperature, but it takes time for this to occur. If we light a fire in one corner of a room, we have to wait a while for the other corners to warm up. Eventually, the room reaches a more or less uniform temperature, but only after the heat from the fire—or, more generally, the information that the fire is there—has had time to spread. Similar reasoning applies to regions A and B in Figure 27.8. They are separated by many megaparsecs, and there has not been time for information, which can travel no faster than the speed of light, to travel from one to the other. In cosmological parlance, the two regions are said to be outside each others' horizon. But if that is so, then how do they "know" that they are supposed to look the same? With no possibility of communication between them, the only alternative is that regions A and B simply started off looking alike—an assumption that cosmologists are very unwilling to make.
The second problem with the standard Big Bang model is called the flatness problem. Whatever the exact value of 0 it appears to be quite close to 1—the density of the universe is fairly near the critical value needed for the expansion barely to continue forever. In terms of spacetime curvature, we can say that the universe is remarkably close to being flat. We say "remarkably" here because again there is no good reason why the universe should have formed with a density very close to critical. Why not a millionth of or a million times that value? Furthermore, as shown in Figure 27.9, a universe that starts off close to, but not exactly on, the critical curve soon deviates greatly from it, so if the universe is close to critical now, it must have been extremely close to critical in the past. For example, if
0 = 0.1 today, then the departure from the critical density at the time of nucleosynthesis would have been only 1 part in 1015 (a thousand trillion).

Figure 27.9 The flatness problem. If the universe deviates even slightly from the critical case, that deviation will grow rapidly in time. For the universe to be as close to critical as it is today, it must have differed from the critical density in the past by only a tiny amount.
These observations constitute "problems" because cosmologists want to be able to explain the present condition of the universe, not just accept it "as is." They would prefer to resolve the horizon and flatness problems in terms of physical processes that could have taken a universe with no special properties and caused it to evolve into the cosmos we now see. The resolution of both problems takes us back in time even earlier than nucleosynthesis or the formation of any of the elementary particles we know today—back, in fact, almost to the instant of the Big Bang itself.
Grand Unified Theories predict that three of the four basic forces of nature—electromagnetism and the strong and weak nuclear forces—are in reality aspects of a single all-encompassing "superforce" (See More Precisely 27-1.) However, this unification is evident only at enormously high energies, corresponding to temperatures in excess of 1028K. At lower temperatures the superforce reveals its separate electromagnetic, strong, and weak characters.
An essential concept in quantum physics is the idea that forces between elementary particles are exerted, or mediated, by the exchange of another type of particle, generically called a boson. We might imagine the two particles as playing a rapid game of catch, using a boson as a ball, as illustrated in Figure 27.10. As the ball is thrown back and forth, the force is transmitted. In ordinary electromagnetism, the boson involved is the photon—a bundle of electromagnetic energy that always travels at the speed of light. The strong force is mediated by particles known as gluons. The electroweak theory includes a total of four bosons: the massless photon and three other massive particles, called (for historical reasons) W+, W-, and Z0, all of which have been observed in laboratory experiments. Most of the particles we have encountered so far in this book—electrons, protons, neutrons, neutrinos—play "catch" with at least some of these "balls."
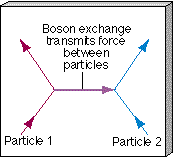
Figure 27.10 Forces between elementary particles are transmitted through the exchange of particles called bosons. As two particles interact, they exchange bosons, a little like playing catch with a submicroscopic ball.
Section 27.1 discussed how particles "froze out" of the universe as its temperature dropped below the threshold temperature for their creation by pair production. Now that we know that the basic forces of nature are also mediated by particles, we can understand—in general terms, at least—how the fundamental forces froze out too as the universe cooled. The W and Z particles responsible for the electroweak force have masses about 100 times the mass of a proton. The threshold temperature for their production—roughly 1015 K—is the temperature at which the weak and electromagnetic forces parted company near the end of the hadron epoch. According to the GUTs, the particle that unifies the strong and electroweak forces is extremely massive—at least 1015 times the mass of the proton, and possibly much more. It is because this particle is so massive that the unification of the strong and electroweak forces becomes evident only at extremely high temperatures.
The freezing out of the electroweak force at a temperature of 1015 K, some 10-10 s after the Big Bang, had little overall effect on the cosmic expansion. By contrast, the freeze-out of the strong force, a mere 10-35 s after the Big Bang, produced one of the strangest events in the history of the cosmos.
As the temperature fell below 1028 K and the strong force appeared for the first time as a separate entity—a little like a gas liquefying or water freezing as the temperature drops—theory implies that the universe briefly entered a very odd, and unstable, high-energy state that physicists call the "false vacuum." In essence, the universe remained in the "unified" condition a little too long, like water that has been cooled below freezing but has not yet turned to ice. This had dramatic consequences. For a short while, empty space acquired an enormous pressure, which temporarily overcame the pull of gravity and accelerated the expansion of the universe at an enormous rate. The pressure remained constant as the cosmos expanded, and the acceleration grew more and more rapid with time—in fact, the size of the universe doubled every 10-34 s or so! This period of unchecked cosmic expansion, illustrated in Figure 27.11, is known as the epoch of inflation.
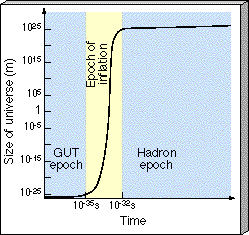
Figure 27.11 During the period of inflation at the end of the GUT epoch, the universe expanded enormously in a very short time. Afterward, it resumed its earlier "normal" expansion rate, except that the size of the cosmos was about 1050 times bigger than it was before inflation.
Eventually, the universe returned to the lower-energy "true vacuum" state. Regions of normal space began to appear within the false vacuum and rapidly spread to include the entire cosmos. With the return of the true vacuum, inflation stopped. The whole episode lasted a mere 10-32 s, but during that time the universe swelled in size by the incredible factor of about 1050. When the inflationary phase ended, the grand unified force was gone forever. In its place were the more familiar electroweak and strong forces that operate around us in the low-temperature universe of today. With the normal vacuum restored, the universe once again resumed its (relatively) leisurely expansion, slowly decelerated by the effect of gravity. But a number of important changes had occurred that would have far-reaching ramifications for the evolution of the cosmos.
The inflationary epoch provides a natural solution to the horizon and flatness problems described earlier. The horizon problem is solved because inflation took regions of the universe that had already had time to communicate with one another—and so had established similar physical properties—and then dragged them far apart, well out of communications range of one another. Regions A and B in Figure 27.8 have been out of contact since 10-32 s after creation, but they were in contact before then. As illustrated in Figure 27.12, their properties are the same today because they were the same long ago, before inflation separated them.
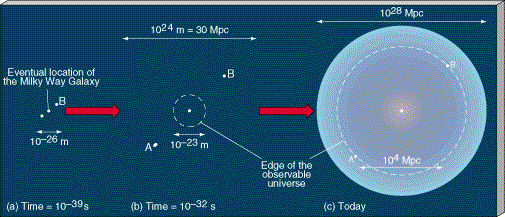
Figure 27.12 Inflation solves the horizon problem by taking a small region of the very early universe, whose parts had already had time to interact with one another and which had thus already become homogeneous, and expanding it to enormous size. In (a), points A and B are well within the (shaded) homogeneous region of the universe centered on the eventual site of the Milky Way Galaxy. In (b), after inflation, A and B are far outside the horizon (indicated by the dashed line), so they are no longer visible from our location. Subsequently, the horizon expands faster than the universe, so that today (c) A and B are just reentering our field of view. They have similar properties now because they had similar properties before the inflationary epoch.
Figure 27.12(a) shows a small piece of the universe just before the onset of inflation. The point that will one day become the site of the Milky Way Galaxy is at the center of the shaded region, which represents the portion of space "visible" to that point at that time—that is, there has been enough time since the Big Bang for light to have traveled from the edge of this region to its center. That entire region is more or less homogeneous because different parts of it have been able to interact with one another, so any initial differences between them have largely been smoothed out. The points A and B of Figure 27.8 are also marked. They lie within the homogeneous patch, so they have very similar properties. The actual size of the shaded region is about 10-26 m—only a trillionth the size of a proton.
Immediately after inflation, as shown in Figure 27.12(b), the homogeneous region has expanded by 50 orders of magnitude, to a diameter of about 1024 m, or 30 Mpc—larger than the largest supercluster. By contrast, the visible portion of the universe, indicated by the dashed line, has grown only by a factor of a thousand and is still microscopic in size. In effect, the universe expanded much faster than the speed of light during the inflationary epoch, so what was once well within the horizon now lies far beyond it. In particular, points A and B are no longer visible, either to us or to each other, at this time. (Note that while the theory of relativity restricts matter and energy to speeds less than the speed of light, it imposes no such limit on the universe as a whole.)
Since then, the universe has expanded by a further factor of 1027, so the size of the homogeneous region of space surrounding us is now about 1051 m (1028 Mpc)—10 trillion trillion times greater than the distance to the most distant quasar. As shown in Figure 27.12(c), the horizon has expanded faster than the universe, so points A and B are just now becoming visible again. As the portion of the universe now observable from Earth grows in time it remains homogeneous because our cosmic field of view is simply reexpanding into a region of the universe that was within our horizon long ago. We will have to wait a very long time—at least 1035 years—before the edge of the homogeneous patch surrounding us comes back into view.
To see how inflation solves the flatness problem, let's return to our earlier balloon analogy. Imagine that you are a 1-mm-long ant sitting on the surface of the balloon as it expands, as illustrated in Figure 27.13. When the balloon is just a few centimeters across, you can easily perceive the surface to be curved—its circumference is only a few times your own size. When the balloon expands to, say, a few meters in diameter, the curvature of the surface is less pronounced, but still perceptible. However, by the time the balloon has expanded to a few kilometers across, an "ant-sized" patch of the surface will look quite flat, just as the surface of Earth looks flat to us.

Figure 27.13 Inflation solves the flatness problem by taking a curved surface, here represented by the surface of the expanding balloon, and expanding it enormously in size. To an ant on the surface, the balloon looks virtually flat when the expansion is over.
Now imagine that the balloon expands 100 trillion trillion trillion trillion times, as the universe did during the period of inflation. Your local patch of the surface is now completely indistinguishable from a perfectly flat plane, deviating from flatness by no more than 1 part in 1050. Exactly the same argument applies to the universe. Any curvature the universe may have had before inflation has been expanded so much that space is now virtually flat, at least on the scale of the observable universe (and, in fact, on much larger scales too).
Notice that this resolution to the flatness problem—the universe looks pretty flat because it is flat—has a very important consequence. Because the universe is flat, the density of matter must be exactly critical: 0 = 1. That means that there must be a lot of invisible matter in the universe beyond the clusters and the superclusters, filling the huge voids on the largest scales. And because we just saw that primordial nucleosynthesis implies that the density of normal matter is at most 3 percent of the critical value, it follows that the rest of the mass—at least 97 percent of all the matter in the universe—must be in the form of dark matter (whatever it may be).
When the idea of inflation was first suggested, most astronomers were very skeptical. Some still are. They point out that there is no observational evidence for a cosmic density as high as the critical value. However, as we saw earlier, there is ample evidence for dark matter in the universe with as much as 20 or 30 percent of the critical density, and estimates of 0 do seem to increase as the scale under consideration increases. Furthermore, inflation is a clear prediction of a group of theories—the GUTs—that are becoming more and more firmly established as the standard description of matter at high energies. If the GUTs are correct, then inflation must have occurred. Finally, inflation provides a neat solution to two serious difficulties with the standard noninflationary Big Bang model. For all these reasons, inflation has become entrenched (albeit as an unwelcome guest in some cases) in most cosmologists' models of the universe. Interlude 27-1 discusses a possibly related, and even more controversial, theory of cosmic expansion.