With humans apparently the only intelligent life in the solar system, we must broaden our search for extraterrestrial intelligence to other stars, perhaps even other galaxies. At such distances, though, we have little hope of detecting actual life with current equipment. Instead, we must ask: How likely is it that life in any form—carbon-based, silicon-based, water-based, ammonia-based, or something we cannot even dream of—exists? The word likely in the last sentence speaks of probabilities. Let's look at some numbers to develop statistical estimates of the probability of life elsewhere in the universe.

THE DRAKE EQUATION

An early approach to this statistical problem is usually known as the Drake equation, after the U.S. astronomer who pioneered this analysis:

Several of the terms in this formula are largely a matter of opinion. We do not have nearly enough information to determine—even approximately—every term in the equation, so the Drake equation cannot give us a hard-and-fast answer. Its real value is that it subdivides a large and very difficult question into smaller pieces that we can attempt to answer separately. It provides the framework within which the problem can be addressed and parcels out the responsibility for the final solution among many different scientific disciplines. Figure 28.7 illustrates how, as our requirements become more and more stringent, only a small fraction of star systems in the Milky Way are likely to generate the advanced qualities specified by the combination of terms on the right-hand side of the equation.

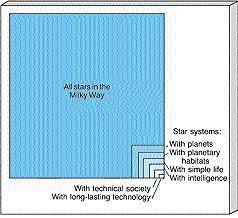
Figure 28.7 Of all the star systems in our Milky Way (represented by the largest box), progressively fewer and fewer have each of the qualities typical of a long-lasting technological society (represented by the smallest box at the lower right corner).

Let's examine the terms in the equation one by one and make some educated guesses about their values. Bear in mind, though, that if you ask two scientists for their best estimates of any given term, you will likely get two very different answers!

RATE OF STAR FORMATION

We can estimate the average number of stars forming each year in the Galaxy simply by noting that at least 100 billion stars now shine in the Milky Way. Dividing this number by the 10-billion-year lifetime of the Galaxy, we obtain a formation rate of 10 stars per year. This may be an overestimate because we think that fewer stars are forming now than formed at earlier epochs of the Galaxy, when more interstellar gas was available. However, we do know that stars are forming today, and our estimate does not include stars that formed in the past and have since exploded, so our value of 10 stars per year is probably reasonable when averaged over the lifetime of the Milky Way.

FRACTION OF STARS HAVING PLANETARY SYSTEMS

Many astronomers believe that planet formation is a natural result of the star-formation process. If the condensation theory (Chapter 15) is correct, and if there is nothing special about our Sun, as we have argued throughout this book, we would expect many stars to have at least one planet. (Sec. 15.2) Indeed, as we have seen, increasingly sophisticated observations indicate the presence of disks around young stars. Could these disks be protosolar systems? The condensation theory suggests they are.

No planets like our own have yet been seen orbiting any other star. The light reflected by an Earthlike planet circling even the closest star would be too faint to detect even with the very best equipment. The light would be lost in the glare of the parent star. Large orbiting telescopes may soon be able to detect Jupiter-sized planets orbiting the nearest stars, but even those huge planets will be barely visible. However, as described in Interlude 15-1, there is now strong indirect evidence that planets are orbiting other stars. Several groups of observers have reported detection of the back-and-forth or side-to-side motions produced in a parent star by an orbiting planet's gravitational pull. The planets found so far are Jupiter-sized rather than Earth-sized, but astronomers are confident that an Earthlike planet will one day be detected by these means. (Recall from Chapter 22 that Earth-mass planets have been observed orbiting some neutron stars. However, as we saw in that chapter, the formation of those planets was very different from that of Earth and the solar system. (Sec. 22.3) They are not thought to be likely candidates for the emergence of life.)

Accepting the condensation theory and its consequences, and without being either too conservative or naively optimistic, we assign a value near 1 to this term—that is, we believe that essentially all stars have planetary systems.

NUMBER OF HABITABLE PLANETS PER PLANETARY SYSTEM

Temperature, more than any other single quantity, determines the feasibility of life on a given planet. The surface temperature of a planet depends on two things: the planet's distance from its parent star and the thickness of its atmosphere. Planets with a nearby parent star (but not too close) and some atmosphere (though not too thick) should be reasonably warm, like Earth or Mars. Planets far from the star and with no atmosphere, like Pluto, will surely be cold by our standards. And planets too close to the star and with a thick atmosphere, like Venus, will be very hot indeed.

Figure 28.8 illustrates that a three-dimensional zone of "comfortable" temperatures—often called a habitable zone—surrounds every star. It represents the range of distances within which a planet of mass and composition similar to those of Earth would have a surface temperature between the freezing and boiling points of water. (Our Earth-based bias is plainly evident here!) The hotter the star, the larger this zone. For example, A- and F-type stars have a rather large habitable zone, but the size of the zone diminishes rapidly as we proceed through G-, K- and M- type stars. O- and B-type stars are not considered here because they are not expected to last long enough for life to develop, even if they do have planets.

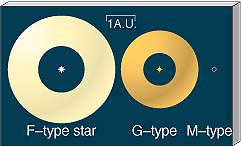
Figure 28.8 The extent of the habitable zone is much larger around a hot star than around a cool one. For a star like the Sun (a G-type star), the zone extends from about 0.85 A.U. to 2.0 A.U. For an F-type star, the range is 1.2 to 2.8 A.U. For a faint M-type star only planets orbiting between about 0.02 and 0.06 A.U. would be habitable.

Three planets—Venus, Earth, and Mars—reside within the habitable zone surrounding our Sun. Venus is too hot because of its thick atmosphere and proximity to the Sun. Mars is a little too cold because its atmosphere is too thin and it is too far from the Sun. But if Venus had Mars's thin atmosphere, and if Mars had Venus's thick atmosphere, both of these nearby planets might conceivably have surface conditions resembling those on Earth.

To estimate the number of habitable planets per planetary system, we first take inventory of how many stars of each type shine in our Galaxy and calculate the sizes of their habitable zones. Then we eliminate binary-star systems because a planet's orbit within the habitable zone of a binary would likely be unstable, as illustrated in Figure 28.9. Given the known properties of binaries in our Galaxy, habitable planetary orbits would probably be unstable in most cases, so there would not be time for life to develop.

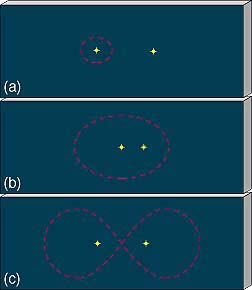
Figure 28.9 In binary-star systems, planets are restricted to only a few kinds of orbits that are gravitationally stable. The orbit in case (a) is stable only if the planet lies very close to its "parent" star, so the gravity of the other star is negligible. Case (b) shows a planet circulating at a great distance about both stars in an elliptical orbit. This orbit is stable only if it lies far from both stars. Another possible, but unstable path, (c) interweaves between the two stars in a figure-eight pattern.

Taking all these factors into account, we assign a value of 1/10 to this term in our equation. In other words we believe that, on average, there is 1 potentially habitable planet for every 10 planetary systems that might exist in our Galaxy. Single F-, G-, and K-type stars are the best candidates.

FRACTION OF HABITABLE PLANETS ON WHICH LIFE ARISES

The number of possible combinations of atoms is incredibly large. If the chemical reactions that led to the complex molecules that make up living organisms occurred completely at random, then it is extremely unlikely that those molecules could have formed at all. In that case, life is extraordinarily rare, this term is close to zero, and we are probably alone in the Galaxy, perhaps even in the entire universe.

However, laboratory experiments (like the Urey—Miller experiment described earlier) seem to suggest that certain chemical combinations are strongly favored over others—that is, the reactions are not random. Of the billions upon billions of basic organic groupings that could possibly occur on Earth from the random combination of all sorts of simple atoms and molecules, only about 1500 actually do occur. Furthermore, these 1500 organic groups of terrestrial biology are made from only about 50 simple "building blocks" (including the amino acids and nucleotide bases mentioned earlier). This suggests that molecules critical to life may not be assembled by pure chance. Apparently, additional factors are at work at the microscopic level. If a relatively small number of chemical "evolutionary tracks" are likely to exist, then the formation of complex molecules—and hence, we assume, life—becomes much more likely, given sufficient time.

To assign a very low value to this term in the equation is to believe that life arises randomly and rarely. To assign a value close to 1 is to believe that life is inevitable, given the proper ingredients, a suitable environment, and a long enough period of time. No easy experiment can distinguish between these extreme alternatives, and there is little or no middle ground. To many researchers, the discovery of life on Mars, Europa, Titan, or some other object in our solar system would convert the appearance of life from an unlikely miracle to a virtual certainty throughout the Galaxy. We will take the optimistic view and adopt a value of 1.

FRACTION OF LIFE-BEARING PLANETS ON WHICH INTELLIGENCE ARISES

As with the evolution of life, the appearance of a well-developed brain is a very unlikely event if only random chance is involved. However, biological evolution through natural selection is a mechanism that generates apparently highly improbable results by singling out and refining useful characteristics. Organisms that profitably use adaptations can develop more complex behavior, and complex behavior provides organisms with the variety of choices needed for more advanced development.

One school of thought maintains that, given enough time, intelligence is inevitable. In this view, assuming that natural selection is a universal phenomenon, at least one organism on a planet will always rise to the level of "intelligent life." If this is correct, then the fifth term in the Drake equation equals or nearly equals 1. Others argue that there is only one known case of intelligence, and that case is life on Earth. For 2.5 billion years—from the start of life about 3.5 billion years ago to the first appearance of multicellular organisms about 1 billion years ago—life did not advance beyond the one-celled stage. Life remained simple and dumb, but it survived. If this latter view is correct, then the fifth term in our equation is very small, and we are faced with the depressing prospect that humans may be the smartest form of life anywhere in the Galaxy. As with the previous term, we will be optimistic and simply adopt a value of 1 here.

FRACTION OF PLANETS ON WHICH INTELLIGENT LIFE DEVELOPS AND USES TECHNOLOGY

To evaluate the sixth term of our equation, we need to estimate the probability that intelligent life eventually develops technological competence. Should the rise of technology be inevitable, this term is close to 1, given long enough periods of time. If it is not inevitable—if intelligent life can somehow "avoid" developing technology—then this term could be much less than 1. The latter possibility envisions a universe possibly teeming with intelligent civilizations but very few among them ever becoming technologically competent. Perhaps only one managed it—ours.

Again, it is difficult to decide conclusively between these two views. We don't know how many prehistoric Earth cultures failed to develop technology, or rejected its use. We do know that the roots of our present civilization arose independently at several different places on Earth, including Mesopotamia, India, China, Egypt, Mexico, and Peru. Because so many of these ancient cultures originated at about the same time, it is tempting to conclude that the chances are good that some sort of technological society will inevitably develop, given some basic intelligence and enough time.

If technology is inevitable, then why haven't other life-forms on Earth also found it useful? Possibly the competitive edge given by intellectual and technological skills to humans, the first species to develop them, allowed us to dominate so rapidly that other species—gorillas and chimpanzees, for example—simply haven't had time to catch up. The fact that only one technological society exists on Earth does not imply that the sixth term in our Drake equation must be very much less than 1. On the contrary, it is precisely because some species will probably always fill the niche of technological intelligence that we will take this term to be close to 1.

AVERAGE LIFETIME OF A TECHNOLOGICAL CIVILIZATION

The reliability of the estimate of each term in the Drake equation declines markedly from left to right. For example, our knowledge of astronomy enables us to make a reasonably good stab at the first term, namely, the rate of star formation in our Galaxy, but it is much harder to evaluate some of the later terms, such as the fraction of life-bearing planets that eventually develop intelligence. The last term on the right-hand side of the equation, the longevity of technological civilizations, is totally unknown. There is only one known example of such a civilization—humans on planet Earth. Our own civilization has presently survived in its "technological" state for only about 100 years, and how long we will be around before a natural or human-made catastrophe (see Interlude 14-1) ends it all is impossible to tell.

One thing is certain: if the correct value for any one term in the equation is very small, then few technological civilizations now exist in the Galaxy. If the pessimistic view of the development of life or of intelligence is correct, then we are unique, and that is the end of our story. However, if both life and intelligence are inevitable consequences of chemical and biological evolution, as many scientists believe, and if intelligent life always becomes technological, then we can plug the higher, more optimistic values into the Drake equation. In that case, combining our estimates for the other six terms (and noting that 10 1 1/10 1 1 1 = 1), we can say

Thus, if civilizations typically survive for 1000 years, there should be 1000 of them currently in existence scattered throughout the Galaxy. If they live for a million years, on average, we would expect there to be a million advanced civilizations in the Milky Way, and so on.