 for the absorbed energy!)
for the absorbed energy!)
 b = 0.04 and
Hubble Constant Ho = 72 km s-1 Mpc-1, what was the proton and electron density at the time of the CMB (assume the gas is fully ionized hydrogen). How much heat energy from the gas enters our unlucky subject at the time of the CMB (when Tgas = Tphotons) from (a) protons, and (b) electrons. How does this compare to the energy coming from the photons?
b = 0.04 and
Hubble Constant Ho = 72 km s-1 Mpc-1, what was the proton and electron density at the time of the CMB (assume the gas is fully ionized hydrogen). How much heat energy from the gas enters our unlucky subject at the time of the CMB (when Tgas = Tphotons) from (a) protons, and (b) electrons. How does this compare to the energy coming from the photons?
(2) Geometry in Curved Spaces :
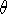 (For example using the Earth, r is from the pole along the surface,
(For example using the Earth, r is from the pole along the surface, 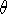 is a change in longitude)
is a change in longitude)
(a) What is ds along a "line of latitude" at constant r from the pole for a small sector d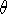 of a circle. Hence, what is the circumference of a circle radius r.
of a circle. Hence, what is the circumference of a circle radius r.
(b) If you can measure lengths to 1 km accuracy (e.g. a car odometer over a long journey), how big must r be to detect the curvature of the Earth by driving around a line of constant latitude (R
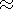 6000 km; assume you know r exactly and your uncertainty is in the circumference).
6000 km; assume you know r exactly and your uncertainty is in the circumference).
(c) What's the relationship between the area of a spherical triangle and the sum of its interior angles (you do not need to derive this relation)? If you can measure angles to 1 arcmin, how big (side length) must an equilateral triangle be to detect the curvature of the Earth?
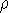 is
roughly Rc2 ~ 3 c2 / (8
is
roughly Rc2 ~ 3 c2 / (8 G
G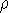 ). Show that this can be re-expressed as
Rc = c × Porb /
). Show that this can be re-expressed as
Rc = c × Porb / 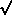 8
8 , where Porb is the period of a circular orbit about the system. [Roughly: Rc
, where Porb is the period of a circular orbit about the system. [Roughly: Rc 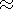 c × dynamical time].
c × dynamical time].
(a) Hence estimate the local spatial radii of curvature (i) near the Earth's surface, (ii) within the solar system (e.g. near the Earth's orbit), (iii) within the galaxy (e.g. near the sun's orbit), (iv) within the universe.
(b) Does this curvature affect metrology with the following levels of accuracy: (a) two satellite GPS triangulation to 1 cm on earth (GPS altitude 20,000 km); (b) wide angle planetary separations to 1 arcsec; (c) wide angle globular cluster separations to 1 arcsec (GC radii out to 50 kpc); (d) angular separations within the local supercluster (50 Mpc) to within 1 arcmin.
(Hint: use the triangle area relation from part c above).
(3) Equations of State
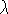 = h / p, which increases with the scale factor, just like light:
= h / p, which increases with the scale factor, just like light: 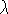
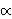 a.
Derive an expression for the equation of state parameter, w, for a gas of these particles, assuming they all have the same mo and p, and that the total energy density is given by u = nE for n such particles per unit volume. Show that in the relativistic limit w
a.
Derive an expression for the equation of state parameter, w, for a gas of these particles, assuming they all have the same mo and p, and that the total energy density is given by u = nE for n such particles per unit volume. Show that in the relativistic limit w 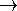 1/3 and in the non-relativistic limit w
1/3 and in the non-relativistic limit w 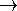 0. (Recall: pressure P = w u = w
0. (Recall: pressure P = w u = w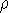 c2 where u =
c2 where u = 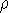 is the total energy density). [Ryden: Q 4.5].
is the total energy density). [Ryden: Q 4.5].
(a) Perfect matter-antimatter symmetry led to full annihilation in the first second.
(b) Something suppressed annihilation, so all CMB photons are instead proton/electron pairs.
(4) Observing De/Acceleration
(5) Proper Distances
(6) Concordance Model
 m = 0.27,
m = 0.27,
 v = 0.73,
v = 0.73,  rel = 8.4 × 10-5, Ho = 72), to plot the following as a function of redshift. Use three
separates graphs for a, b, c. Plot linear z ranges of 0 - 5 for a and b and log z from
-1.0 to 5.0 for c. Mark on each plot the times of matter/vacuum equality (and for c, the time of relativistic/matter equality).
rel = 8.4 × 10-5, Ho = 72), to plot the following as a function of redshift. Use three
separates graphs for a, b, c. Plot linear z ranges of 0 - 5 for a and b and log z from
-1.0 to 5.0 for c. Mark on each plot the times of matter/vacuum equality (and for c, the time of relativistic/matter equality).
You will need to write a routine to evaluate E(z) and its integral. I suggest you make use of the integrator qromb (which also calls trapzd and polint) in Numerical Recipes.
(7) The Age Problem
 m = 0 (empty)
and 1 (flat; Einstein-de Sitter).
m = 0 (empty)
and 1 (flat; Einstein-de Sitter).
 m,o such that tage = 13.0 Gyr -- the
age constraint from GCs. Alternatively, you may solve the parametric equations for an
open pure matter universe, finding
m,o such that tage = 13.0 Gyr -- the
age constraint from GCs. Alternatively, you may solve the parametric equations for an
open pure matter universe, finding 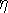 1 such that
a(
1 such that
a(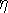 1) = 1, and then finding tage = t(
1) = 1, and then finding tage = t(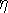 1).
1).
 m,o
m,o 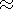 0.3.
What age does this give?
0.3.
What age does this give?
(8) Vacuum Energy's Accelerating Expansion
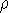 m. What energy resides in the gravitational field of this sphere, i.e., what is it's gravitational binding energy, Ugrav? Why is the sign of Ugrav negative?
m. What energy resides in the gravitational field of this sphere, i.e., what is it's gravitational binding energy, Ugrav? Why is the sign of Ugrav negative?
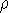 v. Recall that the strange thing about vacuum energy/density is that it is CONSTANT -- when you expand a sphere of it, more of it appears in the new shell. Repeat the evaluation of dUgrav/dR but this time subject to the condition that
v. Recall that the strange thing about vacuum energy/density is that it is CONSTANT -- when you expand a sphere of it, more of it appears in the new shell. Repeat the evaluation of dUgrav/dR but this time subject to the condition that 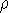 v is constant, not M. Give your answer in terms of M and R (not
v is constant, not M. Give your answer in terms of M and R (not 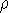 v) What is the sign of dUgrav/dR?
v) What is the sign of dUgrav/dR?
 R2dR
R2dR 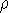 vc2. Find the
expression for dUtot/dR where Utot = Ugrav + Mc2 (again, give your answer in terms of M and R, not
vc2. Find the
expression for dUtot/dR where Utot = Ugrav + Mc2 (again, give your answer in terms of M and R, not 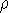 v).
v).
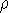 v. For a vacuum density equal to that of water, how big must the sphere be before it continues to expand, making more vacuum as it does so? If the sphere were made of real water (not vacuum), how would it evolve?
v. For a vacuum density equal to that of water, how big must the sphere be before it continues to expand, making more vacuum as it does so? If the sphere were made of real water (not vacuum), how would it evolve?
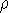 v = 3H2/8
v = 3H2/8 G. Show that the critical radius for
"runaway expansion" is roughly rH, the Hubble radius.
G. Show that the critical radius for
"runaway expansion" is roughly rH, the Hubble radius.
(9) The Flatness Problem
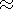 1.3 × 1010 tsec-1/2.
1.3 × 1010 tsec-1/2.
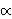 t.
t.
This is an example of how a Universe that is slightly curved (unbound) at early times evolves very differently from a perfectly flat Universe. In this case, the expansion is much faster and reaches the same size (scale factor) and temperature very quickly. [Question 13.3 from Liddle].
(10) The Monopole Problem
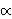 a-3, but the total density, dominated by vacuum, remains fixed. Since that density will be converted to radiation after inflation, we can imagine that the radiation density remains constant during inflation. How much inflationary expansion is necessary so that the present density of monopoles is equal to that of radiation? [Questions 13.5-6 from Liddle].
a-3, but the total density, dominated by vacuum, remains fixed. Since that density will be converted to radiation after inflation, we can imagine that the radiation density remains constant during inflation. How much inflationary expansion is necessary so that the present density of monopoles is equal to that of radiation? [Questions 13.5-6 from Liddle].
(11) Big Bang Nucleosynthesis
(12) Origin of the CMB
nx = gx (mx k T / 2 π ℏ2)3/2 exp[(μx − mx c2) / kT]
Consider the "chemical" recombination reaction: p + e = H + γ. Another fundamental result from statistical mechanics is that when this reaction is in equilibrium, μp + μe = μH + μγ where the general definition of chemical potential is μ/T = (∂S/∂N)U,T (this relation arises from demanding that at a given temperature and energy, the total entropy, S, is at a maximum w.r.t. changing the particle numbers, N, of each species).
Note: Although this treatment seems to follow Ryden (pp 155-159), her MB relation is wrong -- by excluding μ she obscures the true logic behind the derivation of the Saha equation. The correct MB relation, and logic, is taken from Peebles (Principles of Physical Cosmology, pp 165 - 167).
nH / npne = (gH / gpge) (mekT / 2πℏ2)-3/2 exp(Q / kT)
where Q = 13.6 eV is the binding energy of the electron in hydrogen.
Re-express the LHS of the Saha equation in terms of X, η and nγ, and after bringing η and nγ to the RHS, recast nγ explicitly in terms of kT and now simplify the RHS. You should have a quadratic relation for X of the form: (1-X)/X2 = f(η,kT). Hence, show that the ionization fraction, X, is given by:
X = [√(1 + 4f) − 1 ]/2f where f(η,kT) = 3.84 η (kT/mec2)3/2 exp(Q/kT)
In general, optical depth is given by: τ = n σ L, where n is the particle density, σ is the particle scattering cross section, and L is the path length. In our case, σ = σT = 6.6 × 10-25 cm2 is the Thompson cross section; n = ne = X η nγ is the electron density, and L = cΔt is proper path length corresponding to a difference in epoch of Δt. Thus the full expression for optical depth, as a function of redshift is:
τ(z) = 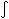 X(z) η nγ σT cdt/dz' dz' where the integral is from z' = 0 to z, and we've transformed our path length, cdt, into a redshift interval.
X(z) η nγ σT cdt/dz' dz' where the integral is from z' = 0 to z, and we've transformed our path length, cdt, into a redshift interval.
Now, although many of these quantities are functions of redshift (e.g. nγ and cdt/dz') the recombination transition occurs over such a narrow window in redshift that we can effectively set these to constants. Thus we have:
τ(E) = σT η nγ cdt/dz' dz'/dT dT/dE 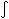 X(E) dE, where E = kT in units of eV.
X(E) dE, where E = kT in units of eV.
Pick a redshift, z, that is in the middle of recombination, and use relations: T = 2.725 (1+z) and T = 11,600 E to obtain values for dz'/dT and dT/dE; and the cosmological relation (see section 6ci): cdt = rH,0 dz / (1+z)E(z) to obtain a value for cdt/dz' (you'll need to use the concordance parameters for E(z), and don't confuse Peeble's E(z) with our energy variable E). Combine all these to get the pre-factor A in the relation τ(E) = A 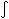 X(E') dE', with limits of E' from 0 to E.
X(E') dE', with limits of E' from 0 to E.
To find the redshift of the cosmic photosphere, where τ(E) = 1, find the value of E such that the integral = 1/A (you will need to do the integral numerically). You should find that the photosphere occurs where X 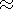 0.1, so the gas that we see in the CMB is in fact pretty neutral.
0.1, so the gas that we see in the CMB is in fact pretty neutral.
(13) Growth of Structure
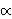 k for small k, passes through a broad peak at k ~ 0.02 (h Mpc-1) and then drops as P(k)
k for small k, passes through a broad peak at k ~ 0.02 (h Mpc-1) and then drops as P(k) 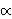 k-3 for large k.
k-3 for large k.
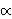 k3 P(k) more useful if we want to consider whether regions of a given size can break away from Hubble expansion and collapse to form objects?
k3 P(k) more useful if we want to consider whether regions of a given size can break away from Hubble expansion and collapse to form objects?