The Astronomer's Universe

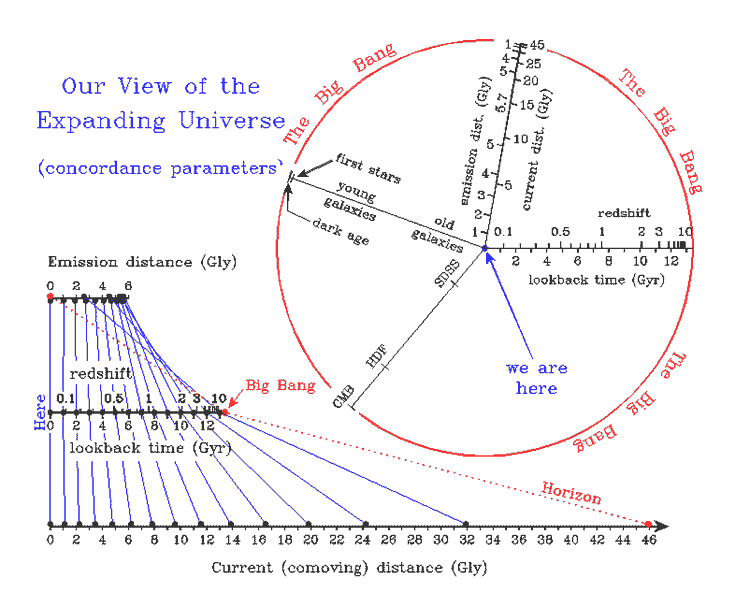
Different presentation of the three principle distances: Current distance: r(t_o); Emission distance: r(t_e); light travel distance: r(lbt)
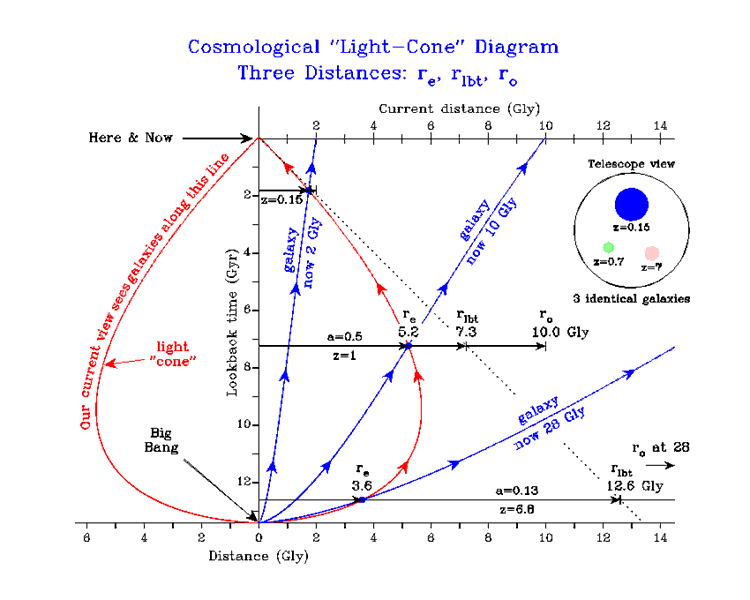
A visually helpful depiction of the Universe, "as we witness it" -- ie looking out is looking back in time. The standard depiction uses "look-back distance" as substitute for the linear time axis. But as the diagram on the left shows (and these curves), this maps non-linearly onto the current (comoving distance), and isn't even monotonic for the distance at emission when the light set out. As you would imagine, the largest look-back times are associated with the most distant current objects, but the light set out when the universe was so much smaller that they were at that time quite close.
Yet another presentation of the three principle distances: Current distance: r(t_o); Emission distance: r(t_e); light travel distance: r(lbt)
This time we're using a "light-cone" space-time diagram (see here). The coordinates are simple linear time for the y-axis, and simple proper distance for the x-axis. The world lines for three objects are shown, at current distances of 2, 10, 28 Gly. The red line is our past light cone -- ie everything we see is situated on this line. Hence the emission distance, r_e is where the world line intersects the light cont; the look-back distance, r_lbt is found by mapping the y-axis across onto the x-axis with a 45 degree line; and the current distance, r_o is found where the world line has time "now". Note the simple depiction of the appearance of three identical galaxies at redshifts 0.15, 0.7, 6.8. Their angular size is determined by r_e and hence gets bigger at great distances. But the surface brighness goes way down because not only is the area larger, but the flux scales with the inverse square of r_o (and a further (1+z)^-2 factor for time dilation and redshift -- see secton 8d). Figures made for this website.