Luminosity is an intrinsic property of a star—it does not depend in any way on the location or motion of the observer. It is sometimes referred to as the star's absolute brightness. However, when we look at a star, we see not its luminosity but rather its apparent brightness—the amount of energy striking a unit area of some light-sensitive surface or device (such as a CCD chip or a human eye) per unit time. Apparent brightness is a measure not of a star's luminosity but of the energy flux produced by the star, as seen from Earth; it depends on our distance from the star. In this section, we discuss in more detail how these important quantities are related to one another.
Figure 17.7 shows light leaving a star and traveling through space. Moving outward, the radiation passes through imaginary spheres of increasing radius surrounding the source. The amount of radiation leaving the star per unit time—the star's luminosity—is constant, so the farther the light travels from the source, the less energy passes through each unit of area. Think of the energy as being spread out over an ever-larger area and therefore spread more thinly, or "diluted", as it expands into space. Because the area of a sphere grows as the square of the radius, the energy per unit area—the star's apparent brightness—is inversely proportional to the square of the distance from the star. Doubling the distance from a star makes it appear 22, or 4, times dimmer. Tripling the distance reduces the apparent brightness by a factor of 32, or 9, and so on.
|
|
|
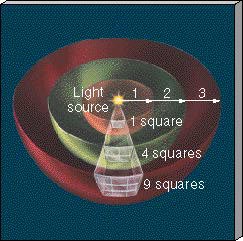 |
Figure 17.7 As it moves away from a source such as a star, radiation is steadily diluted while spreading over progressively larger surface areas (depicted here as sections of spherical shells). Thus, the amount of radiation received by a detector (the source's apparent brightness) varies inversely as the square of its distance from the source.
Of course, the star's luminosity also affects its apparent brightness. Doubling the luminosity doubles the energy crossing any spherical shell surrounding the star and hence doubles the apparent brightness. We can therefore say that the apparent brightness of a star is directly proportional to the star's luminosity and inversely proportional to the square of its distance:
Thus, two identical stars can have the same apparent brightness if (and only if) they lie at the same distance from Earth. However, as illustrated in Figure 17.8, two nonidentical stars can also have the same apparent brightness if the more luminous one lies farther away. A bright star (that is, one having large apparent brightness) is a powerful emitter of radiation (high luminosity), is near Earth, or both. A faint star (small apparent brightness) is a weak emitter (low luminosity), is far from Earth, or both.
Figure 17.8 Two stars A and B of different luminosity can appear equally bright to an observer on Earth if the brighter star B is more distant than the fainter star A.
Determining a star's luminosity is a twofold task. First, the astronomer must determine the star's apparent brightness by measuring the amount of energy detected through a telescope in a given amount of time. Second, the star's distance must be measured—by parallax for nearby stars and by other means (to be discussed later) for more distant stars. The luminosity can then be found using the inverse-square law. This is basically the same reasoning we used earlier in our discussion of how astronomers measure the solar luminosity. (Sec. 16.1)
Instead of measuring apparent brightness in SI units (for example, watts per square meter, the unit used for the solar constant in Chapter 16), optical astronomers find it more convenient to work in terms of a construct called the magnitude scale. The scale dates from the second century b.c., when the Greek astronomer Hipparchus ranked the naked-eye stars into six groups. The brightest stars were categorized as first magnitude. The next brightest stars were labeled second magnitude, and so on, down to the faintest stars visible to the naked eye, which were classified as sixth magnitude. The range 1 (brightest) through 6 (faintest) spanned all the stars known to the ancients. Notice that a large magnitude means a faint star.
When astronomers began using telescopes with sophisticated detectors to measure the light received from stars, they quickly discovered two important facts about the magnitude scale. First, the 1—6 magnitude range defined by Hipparchus spans about a factor of 100 in apparent brightness—a first-magnitude star is approximately 100 times brighter than a sixth-magnitude star. Second, the physiological characteristics of the human eye are such that each magnitude change of 1 corresponds to a factor of about 2.5 in apparent brightness. In other words, to the human eye a first-magnitude star is roughly 2.5 times brighter than a second-magnitude star, which is roughly 2.5 times brighter than a third-magnitude star, and so on. (By combining factors of 2.5, you can confirm that a first-magnitude star is indeed (2.5)5 100 times brighter than a sixth-magnitude star.)
Modern astronomers have modified and extended the magnitude scale in a number of ways. First, we now define a change of 5 in the magnitude of an object (going from magnitude 1 to magnitude 6, say, or from magnitude 7 to magnitude 2) to correspond to exactly a factor of 100 in apparent brightness. Second, because we are really talking about apparent (rather than absolute) brightnesses, the numbers in Hipparchus's ranking system are called apparent magnitudes. Third, the scale is no longer limited to whole numbers—a star of apparent magnitude 4.5 is intermediate in apparent brightness between a star of apparent magnitude 4 and one of apparent magnitude 5. Finally, magnitudes outside the range 1—6 are allowed—very bright objects can have apparent magnitudes much less than 1, and very faint objects can have apparent magnitudes far greater than 6.
Figure 17.9 illustrates the apparent magnitudes of some astronomical objects, ranging from the Sun, at —26.8, to the faintest object detectable by the Hubble or Keck telescopes, an object having an apparent magnitude of 30—about as faint as a firefly seen from a distance equal to Earth's diameter.
Figure 17.9 Apparent magnitudes of some astronomical objects. The original magnitude scale was defined so that the brightest stars in the night sky had magnitude 1, and the faintest stars visible to the naked eye had magnitude 6. It has since been extended to cover much brighter and much fainter objects. An increase of 1 in apparent magnitude corresponds to a decrease in apparent brightness of a factor of approximately 2.5.
Apparent magnitude measures a star's apparent brightness when seen at the star's actual distance from the Sun. To compare intrinsic, or absolute, properties of stars, however, astronomers imagine looking at all stars from a standard distance of 10 pc. There is no particular reason to use 10 pc—it is simply convenient. A star's absolute magnitude is its apparent magnitude when it is placed at a distance of 10 pc from the observer. Because the distance is fixed in this definition, absolute magnitude is a measure of a star's absolute brightness, or luminosity.
When a star farther than 10 pc away from us is moved to a point 10 pc away, its apparent brightness increases and hence its apparent magnitude decreases. Stars more than 10 pc from Earth therefore have apparent magnitudes that are greater than their absolute magnitudes. For example, if a star at a distance of 100 pc were moved to the standard 10-pc distance, its distance would decrease by a factor of 10, so (by the inverse-square law) its apparent brightness would increase by a factor of 100. Its apparent magnitude (by definition) would therefore decrease by 5. In other words the star's absolute magnitude exceeds its apparent magnitude by 5.
For stars closer than 10 pc, the reverse is true. An extreme example is our Sun. Because of its proximity to Earth, it appears very bright and thus has a large negative apparent magnitude (Figure 17.9). However, the Sun's absolute magnitude is 4.8. If the Sun were moved to a distance of 10 pc from Earth, it would be only slightly brighter than the faintest stars visible in the night sky.
The numerical difference between a star's absolute and apparent magnitudes is a measure of the distance to the star (see More Precisely 17-1). Knowledge of a star's apparent magnitude and of its distance allows us to compute its absolute magnitude. Alternatively, knowledge of a star's apparent and absolute magnitudes allows us to determine its distance.