You may not have thought of it before in these terms, but every time you go outside at night and notice that the sky is dark, you are making a profound cosmological observation. Here's why.
According to the cosmological principle, the universe is homogeneous and isotropic. Let's assume that it is also infinite in spatial extent and unchanging in time—precisely the view of the universe that prevailed until the early part of the twentieth century. On average, then, the universe is uniformly populated with galaxies filled with stars. In that case, when you look up at the night sky, your line of sight must eventually encounter a star, as illustrated in Figure 26.3. The star may lie at an enormous distance, in some remote galaxy, but the laws of probability dictate that, sooner or later, any line drawn outward from Earth will run into a bright stellar surface.

Figure 26.3 If the universe were homogeneous, isotropic, infinite in extent, and unchanging, any line of sight from Earth should eventually run into a star, and the entire night sky should be bright. This obvious contradiction of the facts is known as Olbers's paradox.
This has a dramatic implication. No matter where you look, the sky should be as bright as the surface of a star—the entire night sky should be as brilliant as the surface of the Sun! The obvious difference between this prediction and the actual appearance of the night sky is known as Olber's paradox, after the nineteenth-century German astronomer, Heinrich Olbers, who popularized the idea.
What is the resolution to this paradox? Why is it dark at night? We have accepted the cosmological principle, so we believe that the universe is homogeneous and isotropic. We must conclude, then, that one of the other two assumptions (or both)—that the universe is infinite in extent and unchanging in time—is false. Either the universe is finite in extent, or it evolves in time. In fact, the answer involves a little of each and is intimately tied to the behavior of the universe on the largest scales.
We saw in Chapter 24 that all the galaxies in the universe are rushing away from us in a manner described by Hubble's law:
where H0 65 km/s/Mpc is Hubble's constant.
(Sec. 24.5) We used this relation as a convenient means of determining the distances to galaxies and quasars, but it is much more than that.
Assuming that all velocities have remained constant in time, we can ask a simple question: How long has it taken for any given galaxy to reach its present distance from us? The answer follows from Hubble's law. The time taken is simply the distance traveled divided by the velocity, so
For H0 = 65 km/s/Mpc, this value turns out to be about 15 billion years. Notice that the time is independent of the distance—galaxies twice as far away are moving twice as fast, so the time they took to cross the intervening distance is the same.
Hubble's law therefore implies that at some time in the past—15 billion years ago, according to the foregoing simple calculation—all the galaxies in the universe lay right on top of one another. In fact, astronomers believe that everything in the universe—matter and radiation alike—was confined to a single point at that instant. Then the point exploded, flying apart at high speeds. The present locations and velocities of the galaxies are a direct consequence of that primordial blast. This gargantuan explosion, involving everything in the universe, is known as the Big Bang. As best we can tell, it marked the beginning of the universe.
Thus, by measuring Hubble's constant, we can estimate the age of the universe to be 1/H0 15 billion years. The range of possible error in this age is considerable, both because Hubble's constant is not known precisely and because the assumption that galaxies moved at constant speed in the past is not a very good one—in fact, galaxies moved faster in the past; their motion has been slowed by the effects of gravity We will refine our estimate in a moment, but regardless of the details, the critical fact here is that the age of the universe is finite.
This then is the explanation of why the sky is dark at night. Olbers's paradox is resolved by the evolution of the universe itself. Whether the universe is actually finite or infinite in extent is irrelevant, at least as far as the appearance of the night sky is concerned. We see only a finite part of it—the region lying within roughly 15 billion light years of us. What lies beyond is unknown—its light has not yet had time to reach us.
Realize that, even though it appears to place us at the center of the expansion, Hubble's law does not violate the cosmological principle in any way. This can be understood from Figure 26.4, which shows how observers on five separate galaxies might perceive the motion of their neighbors. For simplicity, the galaxies are taken to be equally spaced, 100 Mpc apart, and they are separating in accordance with Hubble's law with H0 = 65 km/s/Mpc. The first pair of numbers beneath each galaxy represents its distance and recessional velocity as measured by the observer on the middle galaxy, number 3.

Figure 26.4 Hubble's law is the same no matter who makes the measurements. The top set of numbers are the distances and recessional velocities as seen by an observer on the middle of five galaxies, galaxy 3. The bottom two sets are from the points of view of observers on galaxies 2 and 1, respectively. In all cases, the same Hubble law holds.
Now consider how the expansion looks from the point of view of the observer on galaxy 2. Galaxy 4, for example, is moving with velocity 6500 km/s to the right relative to galaxy 3, and galaxy 3 in turn is moving at 6500 km/s to the right as seen by observer 2. Therefore, galaxy 4 is moving at a velocity of 13,000 km/s to the right as seen by the observer on galaxy 2. The distances and velocities that would be measured by observer 2 are noted in the second row. Similarly, the measurements made by an observer on galaxy 1 are noted in the third row. Each observer sees an overall expansion described by Hubble's law, and the constant of proportionality—Hubble's constant—is the same in all cases. Far from singling out any one observer as central, Hubble's law is in fact the only expansion law consistent with the cosmological principle.
Let's pause for a moment to take stock of what we have just learned and to shift in a very important way our view of the expansion of the universe as described by Hubble's law. We know when the Big Bang occurred. Is there any way of telling where? The cosmological principle indicates that the universe is the same everywhere, yet we have just seen that the observed recession of the galaxies described by Hubble's law implies that all the galaxies exploded from a point some time in the past. Wasn't that point, then, different from the rest of the universe, violating the assumption of homogeneity expressed in the cosmological principle? The answer is a definite no!
To understand why there is no "center" to the expansion, we must make a great leap in our perception of the universe. If we were to imagine the Big Bang as simply an enormous explosion that spewed matter out into space, ultimately to form the galaxies we see, then the foregoing reasoning would be quite correct—there would be a center and an edge, and the cosmological principle would not apply. But the Big Bang was not an explosion in an otherwise featureless, empty universe. The only way that we can have Hubble's law hold and retain the cosmological principle is to realize that the Big Bang involved the entire universe—not just the matter and radiation within it, but the universe itself. In other words, the galaxies are not flying apart into the rest of the universe. The universe itself is expanding. Like raisins in a loaf of raisin bread that move apart as the bread expands in an oven, the galaxies are just along for the ride.
Let's reconsider some of our earlier statements in light of this new perspective. We now recognize that Hubble's law describes the expansion of the universe itself. Although galaxies have some small-scale, individual random motions, on average they are not moving with respect to the fabric of space—any such overall motion would pick out a "special" direction in space and violate the assumption of isotropy. On the contrary, the portion of the galaxies' motion that makes up the Hubble flow is really an expansion of space itself. The expanding universe remains homogeneous at all times. There is no "empty space" beyond the galaxies into which they rush. At the time of the Big Bang, the galaxies did not reside at a point located at some well-defined place within the universe. The entire universe was a point. That point was in no way different from the rest of the universe; that point was the universe. Therefore, there was no one point where the Big Bang "happened"—because the Big Bang involved the entire universe, it happened everywhere at once.
To illustrate these ideas, imagine an ordinary balloon with coins taped to its surface, as shown in Figure 26.5. (Better yet, do the experiment yourself.) The coins represent galaxies, and the two-dimensional surface of the balloon represents the "fabric" of our three-dimensional universe. The cosmological principle applies to the balloon because every point on the balloon looks pretty much the same as every other. Imagine yourself as a resident of one of the three coin "galaxies" in the leftmost frame, and note your position relative to your neighbors. As the balloon inflates (that is, as the universe expands), the other galaxies recede from you; more distant galaxies recede more rapidly. (Notice, incidentally, that the coins themselves do not expand along with the balloon, any more than people, planets, stars, or galaxies—all of which are held together by their own internal forces—expand along with the universe.)

Figure 26.5 The coins taped to the surface of a spherical balloon recede from one another as the balloon inflates (left to right). Similarly, galaxies recede from one another as the universe expands. As the coins recede, the distance between any two of them increases, and the rate of increase of this distance is proportional to the distance between them. Thus, the balloon expands according to Hubble's law.
Regardless of which galaxy you chose to consider, you would see all the other galaxies receding from you. Nothing is special or peculiar about the fact that all the galaxies are receding from you. Such is the cosmological principle: no observer anywhere in the universe has a privileged position. There is no center to the expansion and no position that can be identified as the location from which the universal expansion began. Everyone sees an overall expansion described by Hubble's law, with the same value of Hubble's constant in all cases.
Now imagine letting the balloon deflate. This corresponds to running the universe backward from the present time to the Big Bang. All the galaxies (coins) would arrive at the same place at the same time—at the instant the balloon reached zero size. But there is no one point on the balloon that could be said to be the place where that occurred. The entire balloon expanded from a point, just as the Big Bang encompassed the entire universe and expanded from a point.
This analogy has its shortcomings. The main difficulty here is that we see the balloon, which in our illustration we imagined as two dimensional, expanding into the third dimension of space. This might suggest that the three-dimensional universe is expanding "into" some fourth spatial dimension. It is not, so far as we know. At the very least, if higher spatial dimensions are involved, they are not relevant to our theory of the universe.
This view of the expanding universe requires us to reinterpret the cosmological redshift. (Sec. 24.5) Up to now we have explained the redshift of galaxies as a Doppler shift, a consequence of their motion relative to us. However, we have just argued that the galaxies are not in fact moving with respect to the universe, in which case the Doppler interpretation is incorrect. The true explanation is that as a photon moves through space its wavelength is influenced by the expansion of the universe. In a sense we can think of the photon as being attached to the expanding fabric of space, so its wavelength expands along with the universe, as illustrated in Figure 26.6. Although it is common practice in astronomy to refer to the cosmological redshift in terms of recessional velocity, bear in mind that, strictly speaking, this is not the right thing to do. The cosmological redshift is a consequence of the changing size of the universe—it is not related to velocity at all.
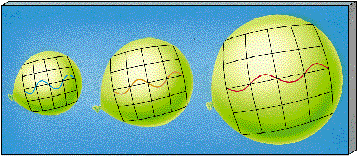
Figure 26.6 As the universe expands, photons of radiation are stretched in wavelength, giving rise to the cosmological redshift.
The redshift of a photon measures the amount by which the universe has expanded since that photon was emitted. For example, when we measure the light from a quasar to have been redshifted by a factor of 5, that means that the light was emitted at a time when the universe was just one-fifth its present size (and that we are observing the quasar as it was at that time). In general, the larger a photon's redshift, the smaller the universe was at the time the photon was emitted, and so the longer ago that emission occurred. Because the universe expands with time and redshift is related to that expansion, cosmologists routinely use redshift as a convenient means of expressing time. (More Precisely 25-1)
These concepts are difficult to grasp. The notion of the entire universe expanding from a point—with nothing, not even space and time, outside—takes some getting used to. Nevertheless, this picture of the universe lies at the heart of modern cosmology. The description of the universe itself (not just its contents) as a dynamic, evolving object is far beyond the capabilities of Newtonian mechanics, which we have used almost everywhere throughout this book. (Sec. 2.7) Instead, the more powerful techniques of Einstein's general relativity, with its built-in notions of warped space and dynamic spacetime, are needed.
We encountered general relativity in Chapter 22 (see especially More Precisely 22-1) when we discussed the strange properties of black holes. We can loosely summarize its description of the universe by saying that the presence of matter or energy causes a curvature of space (more correctly, spacetime) and that the curved trajectories of freely falling particles within warped space are what Newton thought of as orbits under the influence of gravity. The amount of curvature depends on the amount of matter present, and the orbits of particles in turn depend on the curvature. Put less formally, "space tells matter how to move, and matter tells space how to curve." In a homogeneous universe, the curvature of space must be uniform.
Must we keep this difficult notion of a warped, expanding, homogeneous, universe constantly in the forefront of our thoughts if we are to comprehend the evolution of the cosmos? Perhaps surprisingly, given that relativity is the only theory that properly describes the large-scale behavior of the universe, the answer is no. Although general relativity predicts some curious consequences for the overall geometry of space on large scales, as we will see in Section 26.5, the dynamics of the universe can be understood using simple concepts that would have been thoroughly familiar to Newton.
Consider two neighboring points A and B in the expanding universe, as pictured in Figure 26.7. From the perspective of point A, every other point, including B, is rushing away from it, in accordance with Hubble's law. How does the distance between A and B change in time? Does it just keep growing, or does its rate of increase eventually slow down and stop? From a Newtonian viewpoint, we might expect that the overall gravitational pull of the universe would tend to slow the expansion, just as Earth's gravity tends to slow the upward motion of an object projected from the surface. We have just argued that Newtonian physics is inadequate to describe the large-scale dynamics of the universe. However, a surprising prediction of general relativity is that the Newtonian picture gives the right result! The motion of point B relative to point A is exactly the same as if A were at the center of a planet and B were a projectile fired vertically upward from its surface. Thus, we can discuss the expansion of the universe in simple Newtonian terms, but we need general relativity to justify our doing so.
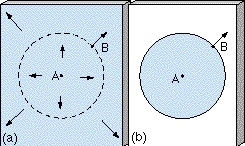
Figure 26.7 The relative motion of any two points in the expanding universe (a) can be addressed as a problem in Newtonian mechanics, even though Einstein's theory of general relativity is needed to explain why it is correct to do so. If the rest of the universe is ignored—as in part (b)—then the Newtonian calculation of B's motion relative to A gives the same answer as a calculation using general relativity.
The Big Bang was a singularity in space and time—an instant when the present laws of physics say the universe had zero size and infinite temperature and density. As we saw in Chapter 22, where we discussed the singularities at the center of black holes, these predictions should not be taken too literally. (Sec. 22.6) The presence of these singularities signals that, under extreme conditions, the theory—in this case, general relativity—making the predictions has broken down.
At present no theory exists to let us penetrate the singularity at the start of the universe. We have no means of describing these earliest of times, so we have no way of answering the question, What came before the Big Bang? Indeed, given the laws of physics as we currently know them, the question itself may be meaningless. The Big Bang represented the beginning of the entire universe—mass, energy, space, and time came into being at that instant. Without time, the notion of "before" does not exist. Consequently, some cosmologists maintain that asking what happened before the Big Bang is like asking what lies north of the North Pole! Others disagree, arguing that one day the proper theory will explain the singularity and allow us to answer the question of what came before.
Although we cannot extend our theory of the universe all the way back to the Big Bang itself, we can come very close. Theorists estimate that the "known" physics of today is adequate to describe the universe since about 10-43 s after the Big Bang. For the purposes of this chapter, at least, 10-43 is close enough to zero that we need not worry about this very early, and completely unknown, epoch.