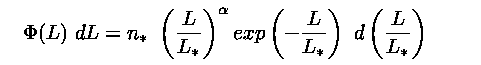Selection of Homework Questions

   

Topic 4: Luminosity Functions

Lets evaluate some basic properties arising from the Schechter Luminosity function of galaxies. First, the function reads:
1. By approximating (L) for just the low luminosity galaxies L << L, show that for -2 < < -1, the total number of galaxies is infinite but the total light is not.

2. Derive an expression for the "mid-rank" galaxy luminosity, L_mid, such that half the light comes from galaxies with L > L_mid and half comes from galaxies with L < L_mid. What is L_mid / L  for = -1 ?

3. Transform the Schechter luminosity function expressed in L to an equivalent function expressed in M, absolute magnitude (don't just copy the formula given in B&M, but show how it comes about).

4. Using whatever computing environment you prefer, generate plots of the following related LFs:

   (a)	Log (L) dL	vs	Log L/L
   (b)	Log (M) dM	vs	M - M
   (c)	Log N(>L)	vs	Log L/L
   (d)	Log N(< M)	vs	M - M

   where the second two are cumulative functions integrated over L or M to brighter galaxies. Take the normalization n to be unity; take the range in L/L to be from 10^-2 to 10; and overplot lines with three values of : -1.5, -1.0, -0.5 (dotted, solid, dashed). Be careful to account for the fact that graph (a) expresses per unit interval of luminosity (dL), while graph (b) expresses per magnitude (dM, which is an interval in Log L). Also, note that graphs (c) and (d) are not expressed per interval, but are integrated, and so they should look the same (excluding, possibly, the direction of the x-axis).

   Summarize, briefly, the various features you see in the plots and their differences. Why does the graph of Log (M) dM  immediately tell you that = -1.0 is the critical value separating finite from infinite numbers of galaxies?

(2) Application to the Coma Cluster :

The Coma cluster of galaxies has a luminosity function which is moderately well represented by the Schechter function, with = -1 and M_B, = -19.2 (H_o = 100 km/s/Mpc). The redshift of Coma is 7000 km/s and its total luminosity is about 250 L.
1. How would and M_B, change if H_o = 50 km/s/Mpc ?

2. What is L (in solar luminosity units) corresponding to M_B, in these two cases (use M_B, = 5.48)

3. Use the total luminosity to evaluate n (the normalization of the Schechter function), and hence estimate how many galaxies are brighter than L,  0.1 L, and 0.01 L.

4. Estimate the expected luminosity of the brightest galaxy, L₁, by setting L₁ equal to the total luminosity expected from the luminosity function in galaxies brighter than L₁. Express L₁ in units of L and as an apparent magnitude. Compare the latter with the observed apparent magnitude for the brightest Coma galaxy, NGC 4889 (B_T^o,i from RC3). Comment on any difference you find between the two magnitudes.