After 2-body relaxation sets in, a different equilibrium power
law distribution arises
There are two competing processes :
- evolution towards isothermality : n(r)
 exp(-
exp(- (r) /
(r) /  2)
2)
near the BH this gives the diverging density
law : n(r)  exp(rBH / r)
exp(rBH / r)
- eating (removing) the stars which get too close to the BH.
Scaling arguments give a density law : n(r)  nc (r / rBH)-7/4
nc (r / rBH)-7/4
this is slightly steeper than the adiabatic growth case described above
2-body scattering at large radii keeps providing stars of
 zero angular momentum to feed the hole
zero angular momentum to feed the hole
the eating rate is given by :
dN/dt  0.013 per year
× MBH,72.33
× nc,41.6
× 0.013 per year
× MBH,72.33
× nc,41.6
×  100-5.76
× M*, 100-5.76
× M*, 1.06
× R*, 1.06
× R*, 1.6 1.6 |
(14.3) |
where the units are indicated by the subscripts (eg nc is in units
of 104 stars pc-3)
Note that for main sequence stars :
for MBH  108
M
108
M , tidal shredding occurs giving
luminous accretion
, tidal shredding occurs giving
luminous accretion
for MBH 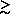 108
M
108
M , stars are swallowed whole, with
no associated luminosity
, stars are swallowed whole, with
no associated luminosity
if AGN luminosity depends on accretion of stars, we might expect :
- low mass spheroids (bulges + Es) : high nuclear densities and low mass
black holes
 high accretion rate
(
high accretion rate
( 10-4 yr-1) of shredded stars
10-4 yr-1) of shredded stars
- high mass spheroids (bulges + Es) : low nuclear densities and high mass
black holes
 low accretion rate
(
low accretion rate
( 10-6 yr-1) of
unshredded stars
10-6 yr-1) of
unshredded stars
 1pc
in size
1pc
in size 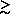 102 -
107 pc-3
102 -
107 pc-3
 all)
all)
 Starburst (rare)
Starburst (rare)
 / dr, which then yields M(r)
/ dr, which then yields M(r) 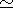 true for galaxy nuclei)
true for galaxy nuclei) ,
,
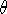 ,
,
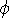 ,
are all functions of radius, r.
,
are all functions of radius, r.  V(r)
V(r)
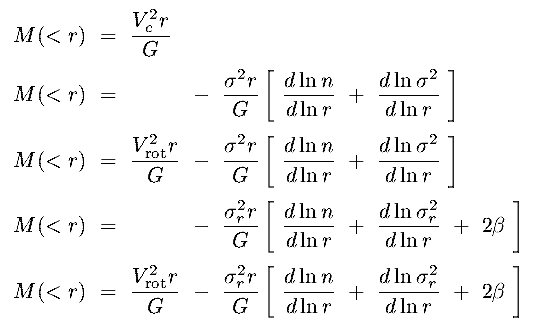

 (similarly for
(similarly for  image indicates a gas disk, rotation
is assumed
image indicates a gas disk, rotation
is assumed  1.35cm allows Doppler velocities to
1 km/s
1.35cm allows Doppler velocities to
1 km/s  no detectable optical or
IR emission from Sgr A*).
no detectable optical or
IR emission from Sgr A*).
 exp(-
exp(- , the equivalent black hole
density is :
, the equivalent black hole
density is :
 BH
BH