Whittle : EXTRAGALACTIC ASTRONOMY




15. ACTIVE GALAXIES & QUASARS
Under Current Construction
: last update April 6 2011


(1) Introduction
(a) Operational Definition of AGN
- Nuclear SMBHs are not sufficient to assign an AGN classification:
e.g. M31 and M32 both have SMBH's but neither show signs activity (accretion power).
- Accreting stellar mass black holes are not AGN -- we need an SMBH located in a galaxy nucleus.
- The activity classification explicitly excludes stars or stellar life cycles
Star formation, HII regions, Supernovae, etc may be present, but they do not constitute an AGN.
- Luminosity isn't part of the definition: activity can be quite weak
For this reason, one often qualifies the power of the AGN, for example:
"QSOs are powerful AGN"; "M81 contains a weak AGN"
- In practice, "evidence for accretion onto an SMBH" means one or more of the following:
- Emission lines with distinct ratios (defined in 3d below) [image].
Often, these are strong & imply photoionizaton by a hard spectrum, rather than by a black body.
- Broad H
 wings or profile (
wings or profile ( 1000
km/s) - i.e. much more than typical galactic velocities. [image].
1000
km/s) - i.e. much more than typical galactic velocities. [image].
- Broad band unresolved continua, with comparable power in X-ray, UV, optical, IR
In the optical, they often appear blue; overall, their continua are unlike starlight. [image]
- Variability of one or more parts of this continuum (or the emission lines)
this points to a highly compact ( 1pc) source of emission [image].
1pc) source of emission [image].
- Radio source, often bipolar & significantly more luminous than in normal galaxies
this may also show jet-like morphology; steep spectrum jet & lobes; flat spectrum core [image].
(b) Reasons for Studying AGN
- The study of AGN started ~50 years ago and now comprises a major branch of astrophysics
A number of factors make AGNs worthy of study:
- At their heart lie giant black holes, perhaps the most exotic astrophysical animal we know of.
AGN give us observational access to these otherwise ellusive objects
- Almost by definition, physical processes near SMBHs are in the relativistic regime
A host of interesting and extreme physical process occur.
While often confusingly complex, they provide a laboratory for studying high energy processes.
- Black hole accretion is very efficient, making AGN amongst the most luminous objects known.
e.g. for mass m in orbit at RS = 2GM/c2, we have 2KE ~ PE ~ GMm/RS = ½mc2
 typical accretion efficiencies are ~¼ mc2
typical accretion efficiencies are ~¼ mc2
this is huge compared to either fusion (~0.7%) or chemical (~10-6%) energy sources.
Accreting just 1 M yr-1 yields
~1046 erg s-1
yr-1 yields
~1046 erg s-1  4 × 1012
L
4 × 1012
L
 200 L
200 L galaxies.
galaxies.
- In addition to photon luminosity, AGN can provide powerful collimated mechanical luminosity.
The creation, propagation and interaction of these jets provide yet another important area of study.
Of course, both accretion flows and jet flows are found in many astrophysical contexts
 AGNs provide excellent windows on both these complex
phenomena.
AGNs provide excellent windows on both these complex
phenomena.
High AGN luminosities yield other important opportunities:
- Luminous AGN can be seen to enormous distances (currently, z~7, lookback time ~95%)
One can therefore study directly their cosmic evolution.
They show strong evolution, with a "hey day" at z~2 (×1000 more common than today).
This evolution is closely tied to early galaxy construction -- another topic of great importance.
- As distant beacons, their spectra provide access to the intervening IGM; for example:
- the highest z QSOs probe the epoch of reionization,
- the transparency of the Lyman continuum proves the IGM is highly ionized
- the ISM in galaxy halos can be analysed throughout much of cosmic history
- the disks of young spirals can also be studied.
- The accretion power ultimately emerges in essentially all spectral wavebands
 AGN present observationally very rich targets
AGN present observationally very rich targets
 they feature in ~all new satellite & instrument observational programs.
they feature in ~all new satellite & instrument observational programs.
- AGN influence 11 decades, from accreting SMBH (~AUs) to jet powered radio lobes (~Mpc)
Of these decades, ~half are observationally unresolvable.
 AGN offer a wonderful window on a huge range of
environments and physical processes.
AGN offer a wonderful window on a huge range of
environments and physical processes.
- With this motivation, let's now begin to look at AGN in more detail
As with all our other Topics, the treatment will be relatively broad and superficial.



(2) Brief Historical Sketch
(a) Early Optical Spectroscopy
1909 : Fath used Lick's Crossley reflector to take spectra of "spiral nebulae"
motivation was to test their extragalactic nature: similar to stars, or MW gas clouds?
most had absorption lines (supports extragalactic); NGC 1068 also had nebula-like emission lines
1917-30 : Slipher, Hubble, Humason confirm Fath's observations & find other examples"
NGC 1275, NGC 4051, NGC 4151.
1943 : Carl Seyfert studied 6 of the 12 known examples in more detail. He found:
- Luminous semi-stellar nuclei [image]
- Nebular spectra of high ionization
- Emission lines broader than either the absorption lines, or HII regions from irregular galaxies
- Forbidden lines narrower than Hydrogen lines in some objects. [image]
Not much notice taken at the time.
1974 : Kahchikian & Weedman argue for Doppler origin for the line-widths; define Sy 1 & Sy 2.
(b) Early Radio Observations
1932 : Jansky discovers radio from the sun & MW
1944 : Reber maps sky @ 160 MHz (1.9 m) & sees peak in Cygnus (Cyg A)
Late 1940s : Post WWII groups @ Manchester; Cambridge (UK); & CSIRO (Australia)
simple interferometry (Michelson & cliff) gives positions & sizes (small) to
 few arcmin.
few arcmin.
 Virgo A = M87; Centaurus A = NGC 5128; Cygnus A = ??
[image]
Virgo A = M87; Centaurus A = NGC 5128; Cygnus A = ??
[image]
Early 1950s : Baade & Minkowski identify Cyg A: "colliding galaxies" [image]
emission lines @ cz=16,830 km/s  high radio luminosity
high radio luminosity
Late 1950s : small double structures; v.high brightness temperatures.
Burbidge applies synchrotron theory  1060 erg ~ 106 M
1060 erg ~ 106 M c2 stored energy.
c2 stored energy.
1974 : Blandford & Rees provide "twin exhaust model" of jets to power the radio lobes.
(c) Quasar Discovery
(d) Redshift Controversy
- High measured z suggests very high luminosity
Rapid variability suggests very small source [ image]
 difficult to believe
difficult to believe  perhaps z is not cosmological?
perhaps z is not cosmological?
- Alternatives: local objects with high gravitational redshifts,
objects with high Doppler velocities, ejected either from the MW or some nearby galaxy.
- Objections to both these, for example:
difficult to explain same z for broad and narrow lines with gravitational redshift
Very high energy for local ejection; why no blueshifts for non-local ejection?
- Evidence grows for cosmological redshift, for example:
Cluster galaxies with same redshift as QSO
Fuzz around some QSOs consistent with host galaxy; ultimately same z measured. [ image]
Highest Seyfert luminosities overlap lower QSO luminosities: continuous population
Today, HST sees host galaxy whenever it "should". Note, it can be difficult to detect because:
- QSOs nucleus often outshines surrounding galaxy
- Rest frame UV of galaxy is much fainter than in the optical for nearby galaxies
- Galaxy surface brightness drops as (1+z)4, making detection difficult.
- Today, cosmological redshifts aren't in doubt, but it was important to check them thoroughly.



(3) The AGN Paradigm
- Before encountering the zoo of AGN species, let's outline their basic anatomical components
Note: not all of these components are apparent/present in any given AGN
The length-scales below refer to a moderately luminous AGN: L ~ 1045 erg s-1, MBH ~ 107.5 M
these lengths probably depend on luminosity: ×10 for QSOs; ×0.1 for weaker AGN.
- A number of "global" figures help:
Figure 1: sketch showing 5 nested scales for Seyferts
Figure 2: single spatial axis with various ranges identified
Figure 3: Blandford's comic-strip of 12 successive scales differing by a factor 10 in scale.
Figure 4: Robson's version of Blandford's comic-strip
Figure 5:
size & waveband axes identifying various emission regions
- Summarizing these, from innermost to outermost scales, we have (plus/minus ½ decade):
Log r
pc | Other | Region/Properties |
| -5 | 2 AU | RS = 2 MBH,8 AU, last stable orbit is 3RS (MBH,8= MBH/108M ) ) |
| -4 | 20 AU | relativistic accretion disk (AD); Fe K line; variable X-ray emission (mins-hours) line; variable X-ray emission (mins-hours) |
| -3 | 200 AU | UV accretion disk; radiation supported AD; |
| -2 | 2000 AU | optical AD; Broad Line Region (BLR); V~104 km s-1; ~few light days. |
| -1 | 0.1 pc | compact, flat-spectrum radio core; VLBI jet; outer BLR |
| 0 | 1 pc | star cusp with velocities affected by BH; dense gas may block some sight lines. |
| 1 | 10 pc | Inner Narrow Line Region (NLR); V  103 km s-1; inner bulge. 103 km s-1; inner bulge. |
| 2 | 100 pc | bulge; NLR; forbidden emission lines; warm dust; VLA jet. |
| 3 | 1 kpc | inner disk; disk ISM; Extended-NLR; Bar & inflow; VLA jet. |
| 4 | 10 kpc | host galaxy; distortions/merger?; ENLR; weak jets blocked. |
| 5 | 100 kpc | near neighbors; tidal influences; powerful jets. |
| 6 | 1 Mpc | jets terminate in IGM hotspots; may affect ICM in cluster. |
- A related summary that considers causal processes goes like this:
- On large scales, galaxy disturbances/mergers are efficient at removing angular
momentum from orbiting gas and this finds its way down to the nuclear regions, possibly
with an associated starburst. Some of this gas may cool and form a dusty thick disk in
the central 1-1000 pc. This gas can obscure our view of the central regions and, conversely, block the outgoing radiation from the AGN along certain directions.
- Ultimately, some of this gas finds its way into an inner accretion disk, whose
Keplerian dynamics is dominated by the black hole. Here, magnetic fields create viscosity
in the disk, which causes the gas to move inwards, releasing gravitational energy which
heats the disk.
The disk has a temperature gradient, and generates at least some of the
optical/UV/X-ray continuum emission via thermal radiation at its surface. Also likely are
non-thermal processes in a disk corona which add to the continuum. Ultimately, gas within
a few RS emits X-rays before crossing the horizon, adding to the mass and angular momentum of the black hole.
- It is in this innermost region that a jet is somehow generated moving out along
the disk axis, probably via magnetic fields tied to the rotating disk. It is not known
why this jet is sometimes very powerful (radio loud AGN), and sometimes much weaker (radio quiet
AGN). The jets are born with bulk relativistic speeds, and contain magnetic fields
and particles with random relativistic speeds -- hence these jets are visible mainly
via synchrotron. The jets burrow out through the
surrounding galaxy ISM with varying degrees of difficulty, entraining and disturbing the
ISM en-route. The most powerful jets can escape the galaxy ISM altogether and traverse
a Mpc before slamming into an outward moving "working surface" of IGM material.
- Returning to the central engine, the accretion process also yields a luminous source of
X-ray, UV, and optical photons, with
roughly power-law spectral shape. This radiation floods out into the galaxy, although some
directions may be blocked by the denser ISM components. Whether or not we get a clear line of sight to the nucleus is thought to explain at least some of the observational variety of AGN.
- The UV-X-ray radiation is an effective ionizer. It first encounters gas clouds within
the central few light days/weeks and the resulting line emission reveals cloud velocities
~103 - 104 km s-1 with gas densities ~1010 cm-3. This emission defines the so-called "Broad Line Region" (BLR). The BLR
velocities are probably gravitational, while the origin of the BLR material is uncertain -- perhaps arising from an accretion disk wind.
- At larger distances, the ISM velocities and pressures both drop. By 10pc - 1kpc
the ionized gas clouds yield velocities ~few ×102 km s-1 -- roughly equal to typical
bulge gravitational speeds -- and gas densities fall from ~106 to ~102 cm-3. This emission defines the so-called "Narrow Line Region" (NLR). Depending
on the geometry of the inner obscuration, the NLR may show bi-conical shape. If jets are blocked in this region, the gas often exhibits significantly higher disturbed velocities.
- Sometimes the jets and ionized gas can be seen to much larger radii, often in association with eachother. The most powerful jets can travel far from the galaxy and
dump their energy in the IGM or, if the galaxy is in a cluster, in the ICM. In that case,
large cavities in the X-ray emission can be seen surrounding the expanding radio source.
- With this outline now in place, we can move on to retrace the rather tangled web
of historical discovery, which led to an equally tangled web of AGN taxonomy. Hopefully,
if you keep the basic anatomy and physiology in mind, you'll be able to clearly navigate
this more historical part.



(4) AGN Taxonomy
(a) Four Basic Criteria
- Over the years, many different categories of AGN have been identified, each with its own name.
In hindsight, this apparent diversity has three distinct components:
- Genuine variation in one or more key properties of AGN
- Apparent variation arising from our particular viewing angle
- Variation which arises from observing the object at a particular stage in its evolution.
- There are (at least) two genuine ways in which AGN differ from eachother:
- UV/opt/IR luminosity: This probably tracks the accretion rate and black hole mass.
Three categories:
Quasars (Lnuc  Lgal);
Lgal);
Strong AGN (Lnuc  Lgal);
Lgal);
Weak AGN (Lnuc << Lgal).
- Radio Luminosity: determined mainly by the jet power
The cause of jet power isn't known : possibly black hole spin and/or disk temperature?
Two categories:
Radio Quiet (LR  10-4 Lopt)
10-4 Lopt)
Radio Loud (LR  10-2 Lopt)
10-2 Lopt)
- There are (at least) two differences which seem to depend on viewing angle [images]
- Emission Line Shapes: do we get a clear view to the inner (BLR) region, or not.
Two categories:
Broad + Narrow lines (can see the BLR)
Narrow lines only (can't see the BLR).
- High variability & high polarization: this depends whether we look directly down a fast jet.
Two categories:
High variability & polarization (look down jet);
Low variability & polarization (look at some other angle).
(b) Taxonomic Table
The following table loosely identifies a number of categories of AGN.
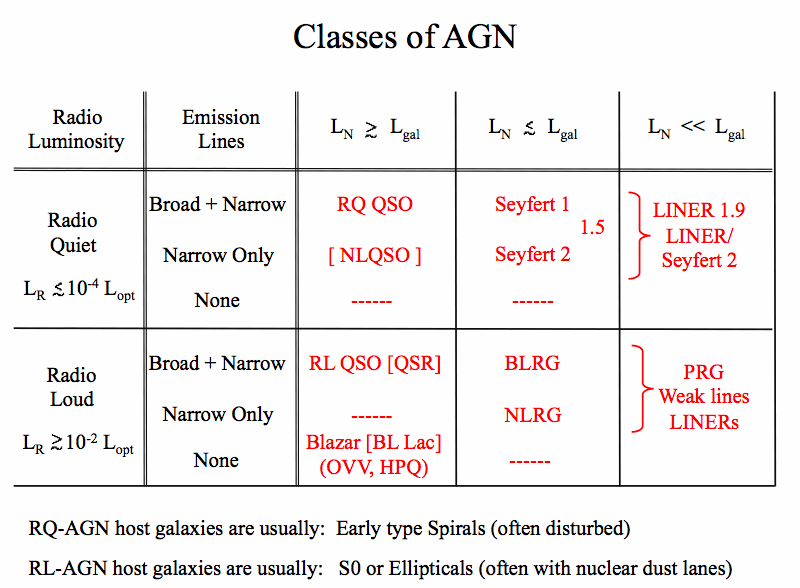
Here are some optical spectra of some of these classes: [image]
Let's define in observational terms some of the various classes;
(some names are not quite standard, but they will help clarify our discussion of
unification)
| Name | Radio | Observational Characteristics |
| Seyfert 1 | RQ | moderate luminosity (MB > -23); strong/visible blue optical continuum; host galaxy clearly visible; broad + narrow lines; narrow lines have high ionization; radio quiet |
| Seyfert 2 | RQ | as for Seyfert 1, but weaker/no blue optical continuum & only narrow lines visible |
| QSO | RQ | Radio quiet quasar; optically luminous (MB < -23); host galaxy barely/not visible; strong optical continuum; broad + narrow lines of high ionization |
| QSO-2 | RQ | same as QSO but missing broad lines; not many currently known (some are IRAS-QSOs) |
| LINER | RQ/L | Low Ionization Nuclear Emission Line Region; weak/no continuum; narrow lines of low ionization & moderate strength; sometimes weak broad H visible; can be either radio quiet or loud visible; can be either radio quiet or loud |
| BLRG | RL | Broad Line Radio Galaxy; similar to Seyfert 1 but radio loud |
| NLRG | RL | Narrow Line Radio Galaxy; similar to Seyfert 2 but radio loud |
| PRG-II | RL | Powerful Radio Galaxy of Fanaroff-Riley class II (edge brightened, powerful jet); unspecified optical spectrum (could be BLRG/NLRG/LINER) |
| RG-I | RL | Similar to PRG-II except lower radio luminosity & Fanaroff-Riley class I (edge darkened, lower power jet) |
| LD-QSR | RL | Lobe Dominated (steep spectrum) Radio Loud Quasar; usually FR-II radio morphology; optically similar to QSO |
| CD-QSR | RL | Core Dominated (flat spectrum) Radio Loud Quasar; optically similar to QSO |
| BL-Lac | RL | Strong featureless continuum, no/weak lines, little starlight; highly variable; high polarization; radio loud flat spectrum core |
| OVV-QSR | RL | Optically Violently Variable Quasar; similar to BL Lac but normal QSO spectrum |
Notes addressing some details:
- Whether QSO-2s exist (optically luminous AGN with no visible BLR) isn't yet clear
A few examples exist, but they seem to be rare.
- The Seyfert 1 - 2 division is continuous; there are intermediates with weak BLRs
In practice, four intermedate designations have been used: [image]
- Seyfert 1.2 : [OIII]5007 / H
 (broad) ~ 1
(broad) ~ 1
- Seyfert 1.5 : [OIII]5007 / H
 (broad) ~ 0.3
(broad) ~ 0.3
- Seyfert 1.8 : H
 (broad) just visible
(broad) just visible
- Seyfert 1.9 : H
 (broad) not visible, but H
(broad) not visible, but H (broad) just visible
(broad) just visible
- Whether all Seyfert 2s have hidden BLRs is still unclear (some certainly do)
There is likely to be an intrinsic range in BLR strength, possibly going down to zero.
NLRs (ionized gas on kpc scales), on the other hand, seem to be ubiquitous.
- The physical nature of LINERs is still under review (see below, in 3d)
There may be (at least) two types, "weak [OI]" and "strong [OI]" LINERs ([OI]
 6300).
6300).
Weak [OI] LINERs may be powered/photoionized by stars (possibly post-AGB stars)
Strong [OI] LINERs usually have weak broad H wings, suggesting a true AGN.
wings, suggesting a true AGN.
In that case, low radiation parameter photoionization by an AGN
matches the spectra well.
- The association of Elliptical/Spiral with radio loud/quiet is still uncertain.
While this seems the case for intermediate/low AGN power, it is less clear for QSOs
(c) Mixed Classifications
- Galaxy nuclei can be both active and have star formation.
What we see (and classify) depends on the relative strength of these contributions
- strong activity can mask weak/moderate star formation
- comparable contributions can lead to mixed classification
- star formation can mask weak activity.
- Regarding mixed objects, there are two contexts worth mentioning.
- At modest luminosity, emission line ratios can lie between those of AGN & HII region
often the two components have different kinematics (line profiles; kpc-scale velocities)
- At high luminosity, many luminous infra-red galaxies (e.g. ULIRGs) may hide a buried QSO.
such objects may be evolving from merger/starburst, to blowout, to exposed QSO (Topic 7).
(d) Emission Line Classification
- Given the various possible types of galactic nuclei, is there a quick/easy way to tell them apart?
 in most cases, the answer is yes, by using the
relative strengths of the narrow lines
in most cases, the answer is yes, by using the
relative strengths of the narrow lines
- Ultimately, different objects contain different sources of ionization with different spectral form.
The resulting ionized regions have different structure and different emission line strengths.
For example, here are four classes of emission line region:
| Object | Ionizing source |
Spectral form |
| PN | Post-AGB star | Black Body, T ~ 35,000K |
| HII region | OB stars | Black Body, T ~ 10,000K |
| Seyfert | strong AGN | Power Law, High U |
| LINER | weak AGN | Power Law, Low U |
- Two important papers introduced ratio-ratio diagrams to separate these classes :
 Baldwin, Phillips & Terlevich (1981 PASP 93, 5)
Baldwin, Phillips & Terlevich (1981 PASP 93, 5)
 Veilleux & Osterbrock (1987 ApJS 63, 295)
Veilleux & Osterbrock (1987 ApJS 63, 295)
the diagrams use only strong lines, and have come to be known as BPT (or VO) diagrams.
BPT use : [OIII]5007 / H ; [NII]6584 / H
; [NII]6584 / H ; [OIII]5007 / [OII]3727; [OIII]5007 / [OI]6300.
; [OIII]5007 / [OII]3727; [OIII]5007 / [OI]6300.
VO use : [OIII]5007 / H ; [NII]6584 / H
; [NII]6584 / H ; [OI]6300 / H
; [OI]6300 / H ; [SII]6717+6731 / H
; [SII]6717+6731 / H
Note that some BPT ratios need reddening correction while the VO ratios don't (being close in  ).
).
- Here's some example spectra and BPT diagrams [image]
In general:
- Seyferts have strong [OIII] / H
 ; strong
[NII] / H
; strong
[NII] / H ; strong [OI] / H
; strong [OI] / H
i.e. a wide range of ionization degree
- LINERs have lower ionization degree: weaker [OIII] / H
 but
strong [NII] / H
but
strong [NII] / H & [OI] / H
& [OI] / H
- HII regions have much weaker [OI] / H
 and somewhat weaker [NII] / H
and somewhat weaker [NII] / H .
.
Some comments:
- HII regions lie along a sequence in metallicity : low Z have higher ionization.
The sequence can reach [OIII] / H ~ 10, so high [OIII]/H
~ 10, so high [OIII]/H is not unique to Seyferts.
is not unique to Seyferts.
- AGNs are different because their ionizing spectra are broad, with a high energy component.
Behind the fully ionized region lie large partially ionized regions kept hot by x-ray heating.
It is in these regions that the [OI], [NII] and [SII] lines are generated efficiently.
- One can think of the Seyfert/LINER group as a single sequence in radiation parameter, U.
e.g. Seyferts: intense hard radiation field  LINERs: weak hard radiation field
LINERs: weak hard radiation field
- Very high ionization lines can be unambiguous indicators of AGN:
e.g. [NeV]3426, since Ne3+ + h
 Ne4+ + e- requires 90 eV photons.
Ne4+ + e- requires 90 eV photons.
- Some non-AGN emission regions can mimick LINER spectra :
e.g. cooling flows; shocks in starburst driven winds; bulge ISM ioinzed by post-AGB stars.
- Fast (500 km/s) shocks can also mimick Seyfert spectra, though no clear cases are known
- Through the 1980s [OIII] linewidth was used in defining AGN (FWHM > 300 km/s)
no more: FWHM tracks bulge mass; many AGN now known with FWHM < 300 km/s.



(5) AGN Detection and Identification
- AGN, particularly luminous ones, are rare - how does one find them?
 search for objects with, e.g., strong radio; UV; emission lines; X-ray.
search for objects with, e.g., strong radio; UV; emission lines; X-ray.
Since AGN differ in their properties,
no method finds all AGN; and
all samples are biassed to some degree.
However, each selection strategy has led to a deeper understanding of the AGN phenomenon.
(a) Radio Surveys
Historically, most early AGNs were discovered from radio surveys at Cambridge & Parkes: e.g.
- 3C (1959) & 3CR (Revised; 1962) cover
 > -5o with
S > 9 Jy @ 178 MHz (328 sources)
> -5o with
S > 9 Jy @ 178 MHz (328 sources)
Note: 1 Jansky = 10-26 W m-2 Hz-1 = 10-23 erg s-1 cm-2 Hz-1
1C & 2C were found to be badly confusion limited, and are never referred to.
4C (1965) had S > 2 Jy; PKS (1965) survey covered the southern sky @ 408 MHz.
- Optical IDs found ~75% radio galaxies ~25% QSOs;
High-z (>2) AGN quite rare, but present; most have steep spectrum (F

 -0.8)
-0.8)
Until ~1970 it was thought all AGN were radio loud;
Then optical surveys find many radio quiet AGN:
Now think only 10% of AGN are radio loud
- Since these early surveys, there have been many others : e.g.
- Green Bank: Northern sky with S > 0.8 Jy @ 1.4 & 5 GHz (1970s)
- Parkes: Southern sky with S > 0.7 Jy @ 2.7 GHz (1970s)
- FIRST: ~¼ full-sky @ 1.4 GHz & 5" beam (VLA-B) S > 1 mJy (~106 sources; 1990s)
- NVSS: ~ 0.8 full-sky @ 1.4 GHz & 45" beam (VLA-C) S > 2 mJy (2 ×106 sources; 1990s)
- 5C: ~15 areas of 10 deg2 with S > 10 mJy @ 408 MHz & S > 2 mJy @ 1.4 GHz (1990s)
- VLA: deep pencil beam surveys: 0.05 deg2 with S > 15 µJy (early 1990s)
- In general, from these surveys one finds:
- The highest flux sources are all powerful AGN.
- The intermediate flux sources are also AGN but of lower luminosity
- The fainter sources include many more normal or starburst galaxies
- At lower frequency (100s MHz) one tends to find large steep spectrum AGN
- At higher frequency (GHz) one tends to find compact flat spectrum AGN
(b) Optical Colors
(i) Single Color
- Bare AGN have much "broader" spectra than stars/galaxies
 UV & IR excesses w.r.t. visible.
UV & IR excesses w.r.t. visible.
In surveys for QSOs, we need to discriminate against stars
From a U-B vs B-V color-color plot a good choice for QSOs is U-B < -0.4 [image]
The main contaminants are hot sub-dwarfs & white dwarfs (O & B stars are too rare to matter).
Here are two well known surveys that used this method:
- BQS : Palomar Bright Quasar Survey (early 1980s; Schmidt & Green).
Used Palomar 48" Schmidt to survey 11,000 deg2 to mB < 16m; select U-B < -0.44
1700 candidates, of which 114 (7%) are AGN (90 have MB < -23, so are classified as QSOs).
These are often referred to as "PG quasars" (Palomar Green).
- Boyle; Shanks; Peterson (~1990) make a similar survey, but much deeper & smaller area
Use UK 48" Schmidt with U & J plates for 7 5o×5o areas to
BJ < 21; select U-B < -0.4
Automated plate scanning finds 1400 UVX candidates; fiber spectroscopy identifies 420 QSOs.
They estimate ~90-95% complete for 0.6 < z < 2.2
- The UVX selection method breaks down for QSOs with z above 2.2
Why? Because Ly enters the B filter, so U-B appears red
enters the B filter, so U-B appears red  confuse with stars
confuse with stars
At even higher z, Ly forest and LyC IGM absorption suppress both U & B
forest and LyC IGM absorption suppress both U & B  ~invisible
~invisible
Notice how N(z) for all known QSOs (c. 1993) closely reflects emission-line influence
on color [image]
- However, at z > 4.2 the IGM absorption makes B-R much redder than ~all stars
 The APM Survey: (Irwin; McMahon; Hazard; 1991) search 2000 deg2 for BJ-R > 3
The APM Survey: (Irwin; McMahon; Hazard; 1991) search 2000 deg2 for BJ-R > 3
Proved to be quite efficient at finding very high-z QSOs.
(ii) Multi-color
- Not surprisingly, ambiguities in U-B for z > 2.2 are removed by including additional colors
A number of such multi-color surveys have been done, especially aiming for high-z QSOs.
Here are just four of them:
- UK Schmidt Survey: (Warren; Hewett; Osmer; 1991) take 6 bands: U,BJ,V,OR,R,I of 43 deg2
Use the APM to scan the plates for stellar objects with 16 < mor < 20  5 colors.
5 colors.
Stars define a "tube" in 5-d space, while QSOs lie outside this space [image].
Ultimately find 85 QSOs with z > 2.2.
- POSS II quasars: (Kennefick et al 1995) use g,r,i plates of 680 deg2
look for Ly in r giving very red g-r for 4.0 < z < 4.8
in r giving very red g-r for 4.0 < z < 4.8
find ~20 QSOs with z > 4 (needs updating)
- Sloan DSS QSOs: Stars define a locus in two color cubes: (u-g, g-r, r-i) and (g-r, r-i, i-z).
QSOs are selected as 4 away, and found in the FIRST radio survey.
away, and found in the FIRST radio survey.
These QSOs are divided into low ( 3) and high (
3) and high ( 3) redshift (see o-link).
3) redshift (see o-link).
(c) Slitless Spectroscopy
- Since AGNs have distinctive optical spectra, is there a way to take spectra of
regions of the sky?
The answer is yes!, and the technique is called slitless spectroscopy
The method is simple, and has a venerable history (1920s HD spectral types for ~105 stars):
- Attach a large prism in front of the entire telescope
- Use Schmidt telescopes + photographic plates
 ~small-ish aperture + large field of view.
~small-ish aperture + large field of view.
- The prism apex angle is small (
 few degrees)
few degrees)  dispersions ~102-103 A/mm at the plate [image].
dispersions ~102-103 A/mm at the plate [image].
Variations in the method use gratings/grisms/grenses, sometimes placed nearer the focal plane
These also give zero-order images  helps measure positions; magnitudes; redshifts
helps measure positions; magnitudes; redshifts
The plates contain thousands of small spectra, to be scrutinized by eye (or machine).
For AGN: look for strong blue/UV continuum &/or emission lines (bright patches)
- Main limitations of slitless surveys are:
- brighter limiting magnitude (since light is dispersed)
- difficulty of completeness estimates, since detection depends on several factors
- bias in favour of strong high equivalent width emission lines
- there are barren redshift ranges with few lines (e.g. z~1, has only MgII 2800)
- spectra may be overlapping in crowded (e.g. low b) fields.
(i) Markarian Survey
- 1967-1981: Byurakan Observatory (Armenia) 1.3m Schmidt surveyed 10,000 deg2
Look for galaxies mB  15.5m with strong UV continuum (term UVX = UV-excess).
15.5m with strong UV continuum (term UVX = UV-excess).
15 lists published containing 1500 "Markarian Galaxies"
Follow-up spectroscopy (mainly by Osterbrock at Lick) found ~10% (~150) Seyferts
Since all have strong UVX, Seyferts divide ~50/50 for types 1/2, with quite luminous Seyfert 2s.
The other 90% are mainly starburst galaxies (strong blue/UV light from OB stars).
- These Markarian Seyferts were a primary target list for studies in the 1970s-80s.
Their virtue is that they provide a sample of relatively nearby (z  0.05) luminous Seyferts.
0.05) luminous Seyferts.
(ii) Other Slitless Surveys
- Since color searches for QSOs fail for z
 2 (see above),
slitless spectra can help.
2 (see above),
slitless spectra can help.
This is astrophysically important, to go beyond the "quasar era" at z ~ 2
Look for rest frame UV lines: Ly 1215; CIV 1550;
CIII] 1909 (eg Ly
1215; CIV 1550;
CIII] 1909 (eg Ly @ 5500A
@ 5500A  z~3.5)
z~3.5)
- LBQS : Large Bright Quasar Survey (1986 - 95; Foltz; Hewett; Chaffee).
Use UK Schmidt & 2o prism & IIIaJ plates to survey 450 deg2
Select for blue continuum (z < 2.2) or spectral features (z > 2.2; limit z~3.4 @ 5400A from IIIaJ)
Find ~1000 QSOs with 16 < BJ < 18.5 and 0.2 < z < 3.4
Sample is ~complete in this brightness & redshift range  good for demographic studies.
good for demographic studies.
- PTGS : Palomar Transit Grism Survey (mid-late 1990s; Schneider; Schmidt; Gunn).
Use 200" & grism & CCDs in drift-scan mode; gives 4400 - 7500A for Ly at 2.5 < z < 5)
at 2.5 < z < 5)
Survey 62 deg2 in six stripes  90 QSOs with
2.75 < z < 4.75
90 QSOs with
2.75 < z < 4.75
 use to show drop in QSO co-moving space density at z > 3.
use to show drop in QSO co-moving space density at z > 3.
(d) Emission Lines
- The previous methods find high levels of activity which dominate the optical light.
What about weaker activity? How does one hunt for that?
One of the most sentitive diagnostics of activity are emission line ratios, for which one needs:
 high S/N ratio spectroscopy of galaxy nuclei, through small apertures.
high S/N ratio spectroscopy of galaxy nuclei, through small apertures.
A number of such surveys have been done, some with AGN detection as goal, some not.
For well defined samples these give the most unbiassed window on AGN demographics
- There have been (at least) four spectroscopic surveys of the nuclei of nearby bright galaxies:
- 1980 Heckman: 100 early type spirals & ellipticals (check) [image]
- 1983 Keel : 100 spirals (check)
- 1984 Stauffer : 80 Spirals (check)
- 1985-95 Ho; Fillipenko; Sargent: 486 galaxies from the RSA (BT < 12.5)
To access weak emission lines, galaxy continuum spectra must often be subtracted (figs)
Emission line ratios are used to establish nucleus type: Seyfert; HII region; LINER.
- From his survey, Heckman identified LINERs = Low Ionization Nuclear Emission Line Regions
While unclear at the time, it is now thought that many of these are weakly active nuclei.
- Using the Palomar survey it is found that (see below for details):
- ~86% of galaxy nuclei have detectable (
 1 A EW) emission lines
1 A EW) emission lines
- ~13% are dominated by Seyfert emission (cf. 2-5% in the Markarian lists)
- ~30% are dominated by LINER emission
- ~40% are dominated by HII emission
 activity is much more common than originally thought, if one includes weak AGN.
activity is much more common than originally thought, if one includes weak AGN.
- Recently, the Sloan & 2dF galaxy redshift surveys have found thousands of new AGN:
These allow a much more definitive analysis of the demographics of galaxy nuclei.
(e) Infra-red
- As discussed in Topic 9.11bv, AGN tend to have "warmer" FIR colors than normal galaxies.
Rather than peaking near 60µm (30K dust) they peak closer to 12-25µm (~100 - 300K)
Moderate luminosity AGN can be selected quite efficiently in the IRAS color-color plot
For example, de Grijp et al (1992) find .... TBD.
(f) X-ray & Gamma-ray
- X-ray emission is obviously an efficient diagnostic for AGNs, especially away from the MW plane
Compared to other wavebands, X-ray surveys have lagged behind somewhat, but are catching up
It is useful to divide X-rays into two bands : soft (0.2 - 2 keV) & hard (2 - 10 keV)
Typical columns to galaxy nuclei may absorb soft, but not hard, X-rays
 soft surveys may miss a significant fraction of the high-column AGN (e.g. Seyfert 2s).
soft surveys may miss a significant fraction of the high-column AGN (e.g. Seyfert 2s).
- There are a number of X-ray surveys which are commonly referenced:
- HEAO-1 all sky (8.2 Sr) 2-10 keV; S > 3×10-11 erg s-1 cm-2 (Piccinotti et al 1982)
85 sources detected; ~60 extragalactic; ~30 clusters; ~30 AGN (Seyfert 1s)
- EMSS (Einstein Extended Medium Sensitivity Survey; Gioia et al 1990)
hunt in 1435 0.3-3.5 keV IPC fields for serendipitous sources
Ultimately, ~800 deg2; varying flux limits; 835 sources; 51% Seyferts & QSOs; 4.3% BL Lacs.
- ROSAT Deep Survey (Hassinger et al 1993) of the "Lockman Hole" (low NH) at 0.5 - 2 keV
~660 sources detected (+ "sky" fluctuations give information on fainter sources)
- ROSAT all sky survey (TBD)
- Chandra Deep Field (TBD)
- There has been one all sky gamma ray survey (Thompson et al 1995)
EGRET on Compton-GRO found 130 sources with S > 10-11 erg s-1 cm-2 at 30 - 3000 MeV;
of these, 40% (~50) were AGN.
(g) Variability & Proper Motion
- It transpires that essentially all AGN are variable.
 variability may provide a relatively unbiassed selection method.
variability may provide a relatively unbiassed selection method.
Also, of course, AGN should have zero proper motion (!)
Hence, a combined criteria will eliminate most variable star contaminators
This method will be used in the upcoming LSST, which should detect 107 AGN.



(6) AGN Demographics
- Overall, how common are the various types of AGN?
As with all astrophysical objects, it depends on luminosity: many more low luminosity AGN.
Our ability to analyse AGN populations depends, to some extent, on the range in luminosity.
(a) Frequency of AGN in the Local Galaxy Population
(b) AGN Preference for Big Bulges
- The spectroscopic surveys also find a link between emission type & Hubble type.
As seen in these histograms: [image]
- HII emission tends to be in late type Spirals, including lower luminosity galaxies;
- LINERs & Seyferts tend inhabit early type Spirals, & avoid low luminosity galaxies
 Activity favours galaxies with relatively luminous bulges.
Activity favours galaxies with relatively luminous bulges.
Similarly, the most luminous early type galaxies (MB  -22) are ~all active.
-22) are ~all active.
(c) Higher Luminosities
- A very rough census of the local populations might go like this:
(Note: 1 Gpc3  sphere radius 620 Mpc
sphere radius 620 Mpc  out to z ~ 0.20h
out to z ~ 0.20h  2 Gyr lookback time)
2 Gyr lookback time)
| Type | # Gpc-3 |
| Galaxies (excl. dwarfs) | 108 |
| Luminous Spirals | 107 |
| Weak AGN | 106.5 |
| Markarian Seyferts | 105 |
| Radio Galaxies | 1000 |
| Radio Quiet QSOs | 100 |
| Radio Loud QSRs | 1 |
Clearly, powerful AGN are locally very rare (e.g. nearest QSR = 3C273 @ 480h-1 Mpc)
At redshift ~2 (10 Gyr ago), luminous AGN were much more common, by ~×1000 (see sec 16)
- More precise discriptions are local AGN luminosity functions
These are usually defined for a given band (radio; optical; X-ray; rarely bolometric)
It is often necessary to combine different samples (e.g. faint & bright), and
correct for various types of bias (see Topic4.4)
Here is one version of the optical luminosity function  (L,z=0): [image]
(L,z=0): [image]
Of course, it is the change of  with redshift that that helps define
AGN evolution (sec 16)
with redshift that that helps define
AGN evolution (sec 16)
- An alternative demographic is the number of AGN per square degree of sky (~5 full moons)
This depends on AGN brightness & waveband, and in part measures a survey's relative efficiency.
Here is N(<B) deg-2 for QSOs, divided into z <2.2 and z > 2.2 [image]
For example, above 21m in B, there are ~30 QSOs with z < 2.2 and ~8 with z > 2.2
@ 22.5m those numbers are 130 & 30, while @ 16m there is ~1 QSO per constellation (10o square).
@ 13m we have one QSO in the whole sky: it is 3C 273.
- Comparing with the other two bands at their approximate current limits :
In X-rays, the ROSAT/EMSS survey finds ~100 AGN deg-2 above 10-14 erg/s/cm2 (0.3-3.5 keV)
In radio, one finds ~25 deg-2 at 5 GHz above 1 mJy (where most sources are still AGN)
While many of the X-ray sources will also be optical QSOs, the radio sources will not.
Surveys in the three main wavebands yield comparable numbers of AGN at their current limits



(7) AGN Unified Schemes
- The huge diversity of AGN can be greatly simplified by first recognizing two intrinsic differences:
- a continuous range of luminosity, from very weak to exceedingly powerful
- a clear division into radio loud (LGHz/Lopt ~ 10-2) and
radio quiet (LGHz/Lopt ~ 10-4)
- Can we gain further simplification by asking how appearance changes with viewing angle?
The answer is yes...., to some extent.
Below we identify various AGN pairings which may differ only by viewing angle
Since viewing angle is essentially arbitrary, this "Unifies" the types involved
- Please note: no-one is suggesting that all AGN are identical !
Just that there may not be quite as many sub-types as originally thought.
(a) Two Different Angle-Dependent Phenomena
(b) Seyfert 2s / Seyfert 1s
(c) NLRGs / BLRGs
- Many of the approaches given above also apply to the NLRG / BLRG objects.
Usually, however, these objects are fainter and more distant and the results are less clearcut.
Here are examples of seeing hidden BLRs in two NLRGs: [image]
(d) Radio Loud: PRG-II / LD-QSR / CD-QSR
First recall there are two types of radio AGN: FR-I and FR-II [image]
To some extent, the unification schemes apply to these types differently.
- It is thought that orientation plays a role in unifying radio galaxies and QSRs: [images]
- It is thought that beaming plays a role in unifying core and lobe dominated QSRs.
(e) RG-I / BL-Lacs : straight down the beam
(f) Intrinsic Differences: Luminosity & Radio Loudness



(8) Accretion Power
- The combination of high luminosity and variability places strong limits on AGN energy sources
 they must be very compact and very efficient
they must be very compact and very efficient
- Hoyle & Fowler (1963) first recognized that gravitational collapse might power AGN engines.
Zeldovich and, separately, Salpter (1964) proposed accretion onto a massive black hole
This became "the AGN paradigm", especially after a nice paper by Lynden-Bell (1974).
- Real accretion is likely to be complex and time varying, with many associated physical processes.
Our discussion will be somewhat idealized -- but it provides a likely overall framework.
- There are a few inter-related themes:
- A natural maximum accretion rate limits AGN luminosity and black hole growth rate
- Even a little angular momentum will ensure the accreting gas forms an accretion disk
- Turbulent viscosity allows gas to lose angular momentum, spiral in, & release energy.
- Black hole spin sets the disk's inner radius which in turn sets the disk's net luminosity.
- Finally, it seems that initial ("seed") black holes will inevitably form in galaxy nuclei.
(a) The Eddington Luminosity & Growth Rate
- Like people, black holes cannot gulp down food with arbitrary speed.
One limitation, which primarily applies to spherical accretion, is due to Eddington (date).
- There is a feedback valve which regulates the accretion flow.
 accretion luminosity generates an outward radiation pressure on the surrounding matter
accretion luminosity generates an outward radiation pressure on the surrounding matter
 this counters the inward gravitational force.
this counters the inward gravitational force.
 if the two are equal, the accretion flow is shut down
if the two are equal, the accretion flow is shut down
- The standard (oversimplified) scenario considers spherical accretion:
A radiation field of energy flux F (erg s-1 cm-2) has momentum flux
(ie pressure) F/c
[note units of F/c: erg cm-3  energy density (Urad)
energy density (Urad)  pressure (Prad)]
pressure (Prad)]
For a single electron, the outward radiation force is:
where  T = 6.65 × 10-25 cm-2 is the Thomson cross section (~independent of E up to ~½MeV)
T = 6.65 × 10-25 cm-2 is the Thomson cross section (~independent of E up to ~½MeV)
- The electrons are strongly tied to the protons, on which gravity principally acts:
Hence the limiting Eddington luminosity, below which gravity "wins" (ie Fgrav = Frad) is:
LEdd = (4 Gcmp)/
Gcmp)/ T × M = 1.26 × 1038 M/M
T × M = 1.26 × 1038 M/M erg s-1 = 3.28 × 104 M/M
erg s-1 = 3.28 × 104 M/M L
L
 Spherically accreting black holes of mass M cannot have luminosities above LEdd
Spherically accreting black holes of mass M cannot have luminosities above LEdd
 Conversely, accretion powered QSOs demand massive (~108 M
Conversely, accretion powered QSOs demand massive (~108 M ) central objects
) central objects
- We may tie this to a maximum (Eddington) accretion rate via the accretion efficiency,
A source with efficiency  radiating at LEdd, accretes matter at a rate:
radiating at LEdd, accretes matter at a rate:
(dM/dt)Edd =  -1 LEdd/c2 = 1.4 × 1026
-1 LEdd/c2 = 1.4 × 1026  0.1-1 M8 gm s-1 =
2.2
0.1-1 M8 gm s-1 =
2.2  0.1-1 M8 M
0.1-1 M8 M yr-1
yr-1
- Do black holes accrete at these maximum rates ?
Estimates of MBH typically find sub-Eddington luminosities: L  0.1 LEdd
0.1 LEdd
- The accretion rate provides a framework for studying black hole growth times
Allowing for sub-Eddington accretion rates, L/LEdd, we have:
dMBH/dt = 2.2  0.1-1 (L/LEdd) × 10-8 M8 M
0.1-1 (L/LEdd) × 10-8 M8 M yr-1
yr-1
yielding exponential growth with e-folding growth times:
tgrowth  4.5 × 107
4.5 × 107  0.1 (LEdd/L) yr
0.1 (LEdd/L) yr
Thus, growth from ~103 to 108 M is ~10 e-foldings
is ~10 e-foldings
 0.5 - 5 Gyr for L/LEdd = 1 - 0.1 which seems reasonable for most AGN
0.5 - 5 Gyr for L/LEdd = 1 - 0.1 which seems reasonable for most AGN
- Some high-z high luminosity QSOs may demand super-Eddington accretion
This is not too problematic.
- Radiate above LEdd by breaking spherical symmetry: equatorial accretion & polar emission.
- Accrete above MdotEdd: optically thick flow traps radiation which is also swallowed.
(b) Thin Accretion Disks
(c) Accretion Efficiency: The Inner Radius
- Because the gravitational potential is so steep at small r, most energy is released in the inner disk.
For this reason, the location of the innermost radius of the disk is crucially important
For finite sized central objects, this is usually the object's surface radius
For black holes, the inner disk radius depends on the black hole's spin (it is NOT just the horizon)
(i) Newtonian Point Mass Potential
- First consider a Newtonian point mass potential:
Let's define the gravitational radius: rg = GM/c2 = distance where PEgrav = -mc2 = -(rest mass)
 one would need a total conversion of rest mass to energy to escape
one would need a total conversion of rest mass to energy to escape  not possible.
not possible.
 rg is very small: rg = 1.5 km M/M
rg is very small: rg = 1.5 km M/M = 1.0 AU M/108M
= 1.0 AU M/108M = 5 mm M/ME
= 5 mm M/ME
- Escape velocity vesc =
 (2GM/r)
(2GM/r)  vesc = c at a radius of 2GM/c2 = 2rg
vesc = c at a radius of 2GM/c2 = 2rg
Michel (1750) recognizes this as an important radius: light can't escape from inside 2rg
By 1920s, this re-emerges as an event horizon for Schwarzchild black holes: rs = 2rg.
- Consider planar orbits in this Newtonian potential. (c.f. discussion in Topic 6.3c)
The radial acceleration equation is (centrifugal - gravity):
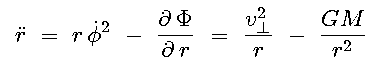 |
(15.1) |
Using the angular momentum per unit mass, h = r×v = r v , we can rewrite this as:
, we can rewrite this as:
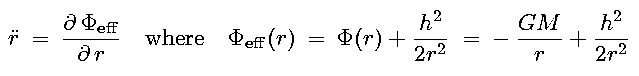 |
(15.2) |
The effective potential,  eff,
allows us to describe the radial motion in 1-D form [image]
eff,
allows us to describe the radial motion in 1-D form [image]
- For Newtonian,
 N,eff is zero at large r,
slowly drops to a minimum before rising steeply at small r
N,eff is zero at large r,
slowly drops to a minimum before rising steeply at small r
Stable circular orbits are found at the minimum in  eff (lowest energy for given h)
eff (lowest energy for given h)
The inner steep term imposes an unsurmountable angular momentum (or centrifugal) barrier
Only when h=0 (a radial orbit) can the trajectory strike the origin.
- Anticipating the relativistic regime, let's re-express 15.2:
- include rest mass, so at large r the potential energy per unit mass
 c2 (not zero)
c2 (not zero)
- divide by c2 to scale all energies relative to rest mass
- express angular momenta relative to rgc, using H = h/rgc per unit mass
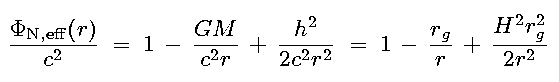 |
(15.3) |
We are now ready to compare this with the effective potential for black holes.
(ii) Schwarzchild (Non-Rotating) Potential
- Schwarzchild (1916) derived the metric for the space-time surrounding a point mass:
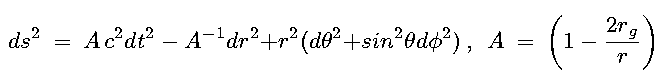 |
(15.4) |
Notice the discontinuity at r = 2rg, and sign change of A when r < 2rg
This radius is called the Schwarzchild radius: rS = 2rg
It marks an event horizon: inside rS all light cones point inwards  a "boundary of no return"
a "boundary of no return"
- The relativistic effective potential per unit mass is given by:
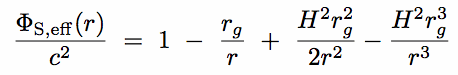 |
(15.5) |
- Comparing
 S,eff with
S,eff with  N,eff we notice several important differences: [see image]
N,eff we notice several important differences: [see image]
- The -(rg/r)3 term ensures an inner turnover
 the central AM barrier is finite
the central AM barrier is finite
 below a certain peri-center distance an orbit is pulled in.
below a certain peri-center distance an orbit is pulled in.
- For H2 > 12,
 S,eff has a minimum
just like
S,eff has a minimum
just like  N,eff, allowing stable circular orbits
N,eff, allowing stable circular orbits
 their radii are: rco = ½rg
[H2 +
their radii are: rco = ½rg
[H2 + 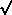 (H4 -12H2)]
(H4 -12H2)]
- For nearly circular orbits, the radial oscillation frequency is:
 2 = (d2
2 = (d2 eff/dr2)rco
[Topic 6.3c]
eff/dr2)rco
[Topic 6.3c]
Unlike the Newtonian case, this does not equal the orbital frequency
 the orbits do not close, but instead precess
the orbits do not close, but instead precess
 this is the origin of the famous precession of the perihelion of Mercury's orbit.
this is the origin of the famous precession of the perihelion of Mercury's orbit.
- For H2 < 12, there are no minima or maxima, so no persistent orbits exist
 at Hcrit = 2
at Hcrit = 2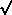 3, the last circular orbit has radius
rlco = ½rgH2 = 6rg = 3rS
3, the last circular orbit has radius
rlco = ½rgH2 = 6rg = 3rS
 circular orbits with r < 3rS simply don't exist, they quickly spiral inwards.
circular orbits with r < 3rS simply don't exist, they quickly spiral inwards.
- In an astrophysical context, gas enters the black hole via an accretion disk
Viscous forces cause gas to slowly migrate to smaller circular orbits, releasing energy on the way
Finally, at r = 3rS the gas plunges into the black hole without dissipation of much further energy.
 the binding energy at 3rS defines the total net accretion efficiency (not at rS)
the binding energy at 3rS defines the total net accretion efficiency (not at rS)
 inserting r = 3rS and H = 2
inserting r = 3rS and H = 2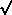 3 into 14.5 gives
3 into 14.5 gives  S,eff /c2 = 0.943
S,eff /c2 = 0.943
 the amount lost is:
the amount lost is:  S,eff(
S,eff( ) -
) -  S,eff(3rS) = (1.0 - 0.943)c2 =
0.057c2
S,eff(3rS) = (1.0 - 0.943)c2 =
0.057c2
 simple accretion onto a Schwarzchild black hole is ~5.7% efficient.
simple accretion onto a Schwarzchild black hole is ~5.7% efficient.
(The simple Newtonian estimate at 3rS is ½ GM/3rs = 8.3% )
(iii) Rotating Black Holes
- Perhaps surprisingly, black holes can have angular momentum: investigated by Kerr (1963)
In this case the metric shows "frame dragging"  a "whirlpool" of space
a "whirlpool" of space
 retrograde pointing rockets must fire to keep "stationary" as seen from afar
retrograde pointing rockets must fire to keep "stationary" as seen from afar
- In addition to the horizon, there is a new "surface": the stationary limit
Inside the stationary limit even light cannot move in a retrograde direction ("flow" of space > c)
The surface has an oblate axisymmetric shape:
rsl = rg × [1 + 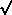 (1 - a2cos2
(1 - a2cos2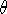 )] [image]
)] [image]
where a measures the BH AM per unit mass: a = (JBH/MBH)/(crg) scaled w.r.t. c rg
(note: a is sometimes defined as a length (Peacock) or mass (Krolik); here it is dimensionless)
- Meanwhile, the true horizon shrinks from the Schwarzchild value of 2rg to:
rh = rg × [1 + 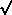 (1 - a2)]
(1 - a2)]
Note that rh is spherical, and meets rsl at the poles.
- Plots of
 K,eff (not shown) for a rotating BH are similar to
those of the Schwarzchild case:
K,eff (not shown) for a rotating BH are similar to
those of the Schwarzchild case:
 circular orbits are allowed down to a last minimum radius, rlco
circular orbits are allowed down to a last minimum radius, rlco
 as AM increases, rlco decreases (increases for retrograde).
as AM increases, rlco decreases (increases for retrograde).
There is a hard upper limit to AM: a = 1, for which rlco = rg (9 rg for retrograde)
Inserting a = 1 and r = rg into  K,eff yields a binding energy of 42% mc2
K,eff yields a binding energy of 42% mc2
(the simple Newtonian efficiency is ½GM/rg = 50%)
In reality, optimum conditions can only create a = 0.998, which drops the yield to ~30%.
Thus, the range a = 0  0.998 yields accretion efficiencies
6 - 30%
0.998 yields accretion efficiencies
6 - 30%
Hence, the often used value, 
 10%
10%
- These efficiencies can yield enormous luminosities with only modest accretion rates:
consider: 1 M yr-1 = 2 × 1033 / 3.17 × 107 = 6.3 × 1025 gm s-1 (ME every 2 minutes)
yr-1 = 2 × 1033 / 3.17 × 107 = 6.3 × 1025 gm s-1 (ME every 2 minutes)
giving: 5.7 × 1045  0.1 M/M
0.1 M/M yr-1 erg s-1 (
yr-1 erg s-1 ( 1.4 × 1012 L
1.4 × 1012 L
 100 L
100 L galaxies)
galaxies)
 easily enough to power QSOs.
easily enough to power QSOs.
Whether black holes can actually gorge themselves so fast is discussed below.
(d) Feeding the Disk
(i) Nuclear ISM
- TBD
(ii) Tidally Disrupted Stars
- Black hole sizes grow in proportion to their mass: rh
 MBH
MBH
This is unusual :
constant density solids have r  M1/3,
degenerate matter has r
M1/3,
degenerate matter has r  M-1/3
M-1/3
 black holes get "bigger" quickly
black holes get "bigger" quickly
- Their mean density drops: <
 BH>
BH>
 M / (4/3
M / (4/3 rh3)
rh3)
 1.7 M8-2 gm cm-3 (Schwarzchild hole).
1.7 M8-2 gm cm-3 (Schwarzchild hole).
Obviously, for 1-few M the mean density is huge, but SMBH are about like water !
the mean density is huge, but SMBH are about like water !
- Tidal stretching forces behave in a similar way:
Newtonian analysis: T = dF/dr = 2GM/r3  10-6 M8-2 N m-1 at the horizon
10-6 M8-2 N m-1 at the horizon
Again, for 1-few M , T ~ few million tons per meter; while for an SMBH it is imperceptible
, T ~ few million tons per meter; while for an SMBH it is imperceptible
 you could happily fall into an SMBH and survive much of the journey to the singularity.
you could happily fall into an SMBH and survive much of the journey to the singularity.
- Of more astrophysical interest: are stars tidally destroyed before or
after entering the horizon?
Before: the material will enter the accretion disk and liberate energy on the way in
After: the star is already lost and its infall goes essentially unnoticed.
- The Roche criteria for tidal breakup of a self-gravitating object is discussed in Topic 12.3bi
Breakup occurs if the mean density within the orbit is greater than the mean density of the orbiter
Now, the mean black hole density within rh is 1.7  14 M8-2 gm cm-3 (Schwarzchild
14 M8-2 gm cm-3 (Schwarzchild  Kerr).
Kerr).
Whereas A0  M0 main sequence stars have <
M0 main sequence stars have < >
>  0.2
0.2  2
2 

 0.3
0.3  3 gm cm-3
3 gm cm-3
 Black holes with M
Black holes with M  few × 108 will start swallowing main sequence stars whole.
few × 108 will start swallowing main sequence stars whole.
However, giant stars are 10 - 100 times R , with
<
, with
< > ~ 10-4 - 10-5
> ~ 10-4 - 10-5 

 Giant stars, while much rarer, are essentially always disrupted
Giant stars, while much rarer, are essentially always disrupted
(e) Extracting Rotational Energy?
- Previous estimates of engine efficiency,
 , express this relative to the infalling mass.
, express this relative to the infalling mass.
One factor which limits  is the final KE of the accreted mass: it is lost to the black hole.
is the final KE of the accreted mass: it is lost to the black hole.
Is there a way to recover any of this energy, perhaps by "slowing" down the hole?
- First let's see how much energy is actually available.
The mass/energy of a rotating hole is in two forms: rotational energy & irreducible mass
For a maximal Kerr hole (a = 1) it is found that Mirr = MBH /  2
2  0.71 MBH
0.71 MBH
Hence, the total available for extraction is 29% of MBH: a significant amount!
- A purely dynamical process was suggested by Penrose (1969)
Between rh and rsl lies the ergosphere: "ergo" = work/energy
Within this region, imagine throwing an object "upstream" in a retrograde direction
 space pushes everything prograde: the object falls in & you recoil and escape
space pushes everything prograde: the object falls in & you recoil and escape
 you slowed the BH (a bit) and extracted some of its rotational energy!
you slowed the BH (a bit) and extracted some of its rotational energy!
Unfortunately, the high "throw speed" required by this process is unlikely to occur naturally.
- An MHD process was suggested by Blandford & Znajek (1977)
TBD
(f) Inevitability of Black Hole Formation
Since QSOs were common at z~2-4, supermassive black holes must form quite quickly.
There is currently much work on how this might have occurred, with no clear consensus.
Perhaps the first stars die to form the first black holes, which then grow by accretion?
Perhaps large gas clouds collapsed directly to form massive black holes?
Here is a famous figure by Martin Rees that shows many paths to forming Massive Black Holes: [image]



(9) Continuum SEDs



(10) Emission Line and Ionized Cloud Physics
Ionizing radiation from the central engine enters surrounding gas and ionizes it.
There are a number of simple phenomena related to this ionized gas worth discussing.
Recall, there are two emission regions in our standard picture: the BLR and the NLR
[image]
How do we find out the properties of the gas in these regions?
(a) Simple Density Limits for the NLR and BLR
There are two kinds of emission lines:
- Recombination lines (e.g. Balmer H lines).
These transitions are electric dipole, so occur easily,
 they have very short lifetimes, and are called "permitted" transitions.
they have very short lifetimes, and are called "permitted" transitions.
- Collisionally excited lines: ground state often split by small energies
 E ~ kT
E ~ kT
 thermal collisions can populate these low lying levels.
thermal collisions can populate these low lying levels.
De-excitation occurs either by collisions or radiatively & which dominates depends on which occurs fastest.
Often, the radiative lifetimes are long, because the transitions are "forbidden"
(only occur via electric quadrupole or magnetic dipole transitions).
 tend to be suppressed at high densities, when collision times are fast.
tend to be suppressed at high densities, when collision times are fast.
At the critical density, the radiative and collisional rates are equal.
In gas with density above the critical density, the line is not strongly produced (collisionally suppressed).
Here are some (Log) critical densities, in cm-3, for some important emission lines:
| C III] 1909 | 9.0 | [Fe VIII] 5159.0 | 6.5 |
| [O II] 3726.1 | 3.5 | [N II] 5754.6 | 7.5 |
| [O II] 3728.8 | 2.8 | [O I] 6300.3 | 6.3 |
| [Ne III] 3868.8 | 7.0 | [Fe X] 6374.6 | 9.7 |
| [Ne III] 3967.5 | 7.0 | [N II] 6583.4 | 4.9 |
| [O III] 4363.2 | 7.5 | [S II] 6716.4 | 3.2 |
| [O III] 5006.9 | 5.8 | [S II] 6730.8 | 3.6 |
- We can use these to get rough estimates of the gas density in the NLR and BLR:
NLR BLR
Forbidden Lines: yes no e.g. [OIII] 5007 (Ncr ~ 106)
Semi-forbidden Lines: yes yes e.g. CIII] 1909 (Ncr ~ 109)
Permitted Lines: yes yes e.g. H , H
, H
 density ne cm-3
density ne cm-3  104-6
104-6  107.5 (absence of, e.g., [OIII] 4363)
107.5 (absence of, e.g., [OIII] 4363)
 109 (presence of [CIII 1909)
109 (presence of [CIII 1909)
Of course, a range of densities is likely present in both regions.
 In fact, other evidence suggests at least some BLR gas has ne ~ 1011.
In fact, other evidence suggests at least some BLR gas has ne ~ 1011.
(b) Properties of a Homogeneous Gas at Single ne and Te
Temperature sensitive line ratios have two upper levels with  E
E  kT
kT
 collisional excitation favors the lower level by exp(-
collisional excitation favors the lower level by exp(- E / kT)
E / kT)
 the line from this level is relatively stronger at lower temperature.
the line from this level is relatively stronger at lower temperature.
A good example is [OIII] 5007 / 4363 [image]
Density sensitive line ratios have two upper levels with  E
E  kT
kT
 collisional excitation gives equal populations
collisional excitation gives equal populations
However the line strengths differ due to their different critical densities.
A good example is [SII] 6717 / 6731 [image]
Of course, in detail, the line ratios are functions of both temperature and density [image]
One can then use various line ratios to hunt for a single combination of ne and Te [image]
This is only justified for a single emission region with uniform properties (not, usually, an entire NLR).
(c) The Structure of Ionized Clouds
The NLR and BLR are thought to contain clouds that are photoionized by the central UV-X-ray source.
The clouds are optically thick to the ionizing Lyman continuum.
 This leads to a layered cloud structure:
This leads to a layered cloud structure:
highly ionized front; decreasing ionization into the cloud; neutral/low ionization back [image].
For a black body spectrum, ionization degree ~uniform up to Stromgren depth, then neutral.
For a power-law (AGN) spectrum, wide range of ionization & extended partially ionized region.
 wide range of excitation (e.g. [OIII] and [OI] lines strong).
[image]
wide range of excitation (e.g. [OIII] and [OI] lines strong).
[image]
There is a long history of computing the structure and emergent spectrum from photoionized gas clouds.
The most widely used code is "CLOUDY", written by Gary Ferland [o-link1 and o-link2]
[Here is a nice vignette of its 1978 origins at the IoA Cambridge].
(d) The Radiation Parameter
The most important parameter governing the emission from photoionized gas is the radiation parameter.
It is defined by the ratio of ionizing photon density to electron (gas) density at the front of the cloud:
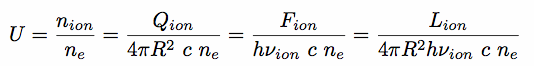 |
(15.6) |
where, more precisely, Qion =  L
L / h
/ h d
d from the Lyman limit to infinity.
from the Lyman limit to infinity.
Basically, higher U gives more highly ionized gas, for the obvious reason:
greater photon density causes higher rates of ionization
greater electron density causes higher rates of recombination
 Their ratio sets the equilibrium ionization degree.
Their ratio sets the equilibrium ionization degree.
The emitted spectrum from a single cloud changes with U as you'd expect:
High U  stronger high ionization lines (e.g. [OIII], CIV etc)
stronger high ionization lines (e.g. [OIII], CIV etc)
Low U  stronger low ionization lines (e.g. [OI], [SII] etc)
stronger low ionization lines (e.g. [OI], [SII] etc)
Here are some calculated line strengths for a sequence of models with different U: [image]
(e) Calculating Simple Region Properties
Some simple relations yield estimates for some emission region properties
The examples used here are for a typical BLR.
(i) Mass of Ionized Gas
- Simple recombination physics gives the luminosity of H
 :
:
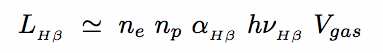 |
(15.7) |
where  H
H = 3.0 × 10-14 cm3 s-1 is the recombination coefficient for H
= 3.0 × 10-14 cm3 s-1 is the recombination coefficient for H (at T = 104K).
(at T = 104K).
This gives Vgas (ionized gas volume) using measured values for H luminosity and gas density (ne
luminosity and gas density (ne  np).
np).
- This now gives the mass of ionized gas: Mgas
 Vgas np mp.
Vgas np mp.
This gives ~1 M for the BLR and ~ 106 M
for the BLR and ~ 106 M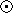 for the NLR
for the NLR
(ii) Region Size
Line ratios yield an estimate for the radiation parameter, U (see section 10d above).
Knowing U, Qion, and ne now gives R, the distance from the ionizing source to the line emitting gas.
Using ne ~ 109.5 for the BLR gives R ~ 0.1 - 1pc and ne ~ 105 for the NLR gives R ~ 100 - 1000pc
[Note: this BLR size is larger than from time delay analysis -- see below, section 11.?]
(iii) Filling Factor of Ionized Gas
The filling factor for the ionized gas is defined to be Vgas / Vregion
Typical values suggest the filling factors are small ~ 10-4
 The regions contain relatively small clouds, within an intercloud medium.
The regions contain relatively small clouds, within an intercloud medium.
(iv) Cloud Size
- A simple estimate for the depth of the ionized region is given by the Stromgren Depth, dS
Balancing the total ionizations with total recombinations, per unit area, we have: [image]
 |
(15.8) |
This yields relatively small clouds: ~1012 and 1014 cm for the BLR and NLR respectively.
- What about the more neutral region behind the Stromgren depth?
In AGN BLR clouds, this is partially ionized by X-rays and heated by photo-ejected electrons
Matching line ratios yields a total column density ~ 1022-23 cm-2
 Using a cloud density then yields cloud diameter ~1013-14 cm for the BLR (~ 1 AU).
Using a cloud density then yields cloud diameter ~1013-14 cm for the BLR (~ 1 AU).
These are small compared to the region size, confirming the low filling factor.
(v) Cloud Numbers
Taking the volume of ionized gas to be ~dS3, we have for the number of clouds:
Ncl  Vgas / dS3
Vgas / dS3  1010
1010
This is only a rough estimate because we've ignored the neutral material.
But the overall conclusion is: a region sparsely filled with many optically thick line emitting clouds.



(11) The Broad Line Region
See Peterson Review: here
High density and anisotropic cloud emission: o-link



(12) The Narrow Line Region



(13) Intrinsic Absorption Lines



(14) AGN Radio Properties : Cores, Jets, Lobes
Compilation of double radio sources by Leahy & Bridle is here: [o-link]
Paper on collimation in M87 is here
More high res (7mm VLBA) on nearby RGs is here



(15) AGN Host Galaxies and Environment


(16) AGN Evolution
include source counts; V/Vmax (Krolik ch 3)




 wings or profile (
wings or profile (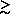 1000
km/s) - i.e. much more than typical galactic velocities. [
1000
km/s) - i.e. much more than typical galactic velocities. [ 1pc) source of emission [
1pc) source of emission [ typical accretion efficiencies are ~¼ mc2
typical accretion efficiencies are ~¼ mc2  yr-1 yields
~1046 erg s-1
yr-1 yields
~1046 erg s-1  4 × 1012
L
4 × 1012
L galaxies.
galaxies.


 , H
, H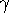 , H
, H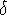 , H
, H @ z=0.16 and can therefore identify MgII 2800.
@ z=0.16 and can therefore identify MgII 2800. 
 6300).
6300).  away, and found in the FIRST radio survey.
away, and found in the FIRST radio survey.  0.1) are probably genuine weak AGN
0.1) are probably genuine weak AGN
 0.1) are probably photoionized by stars
0.1) are probably photoionized by stars
 sphere radius 620 Mpc
sphere radius 620 Mpc  (L,z=0): [
(L,z=0): [
 d2 × 1.8 × 10-11 [13.5S12 + 5.2S25 + 2.6S60 + S100] erg s-1 (
d2 × 1.8 × 10-11 [13.5S12 + 5.2S25 + 2.6S60 + S100] erg s-1 ( v path through dense gas exposed to strong pumping radiation
v path through dense gas exposed to strong pumping radiation
 (2GM/r)
(2GM/r) 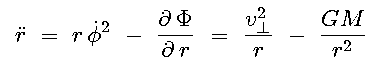
 , we can rewrite this as:
, we can rewrite this as:
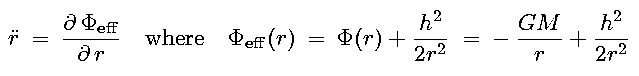
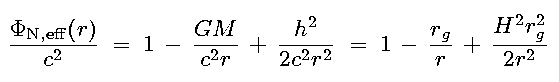
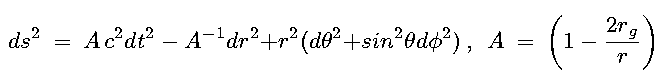
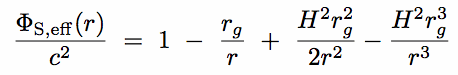
 2 = (d2
2 = (d2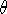 )] [
)] [ BH>
BH>
 L
L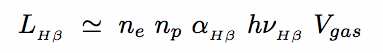
 for the BLR and ~ 106 M
for the BLR and ~ 106 M