Whittle : EXTRAGALACTIC ASTRONOMY




1. HISTORY & PRELIMINARIES


(1) Introduction
Let's start this course with the suggestion that the subject is of fundamental
importance.
For reasons not yet fully understood, matter in the universe is organized
into three basic structures:
- Atoms
- Stars
- Galaxies -- the subject of this course
Our understanding of each has grown in rough synchrony :
- ~1750 - 1850 : recognition of basic existance
- ~1850 - 1930 : recognition of basic properties
- ~1930 - present : deeper understanding (structure, creation, evolution,
sociality)
It is probably fair to say that our understanding of galaxies has lagged
behind atoms and stars,
mainly because they are difficult to observe, being so faint.
Let's first look briefly at some historical hightlights.



(2) Discovering Galaxies : Ours & Others
(a) Early Aims
- Early thinking (before 1923) focussed on two main questions :
- What is the Milky Way (Latin : Via Lactea)
- initially : what is its shape and where is the sun
- later : what is its size and internal motion
- What are the Nebulae (Latin : clouds)
- initially : use "large" telescopes to find, catalog, and describe them
- later : are they unresolved star groups, or genuinely nebulous (gaseous)
- finally : are they internal to the MW, or external "island
universes"
- As telescope apertures increased, the methods developed :
- Visual
 photographic
photographic
 visual spectra
visual spectra  photographic spectra
photographic spectra
- The path of discovery was NOT linear, with discussion often polarized
and ambiguous.
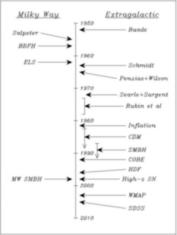
- Here are some simple time-line sketches identifying the key people/work
(b) Before 1850 : Search & Discovery
(c) 1850 - 1925 : The Great Debates
- 1864-68 : William Huggins (English) :
[image]

telescopic visual spectra of nebulae
1/3 emission lines (gaseous); 2/3 continuous (stellar)
- 1888 : John Dreyer (Danish) [image] working
at Birr Castle, compiles

New General Catalog (NGC) : 7840 nebulae
Index Catalog (IC) : 5086 more
- 1900s : James Keeler and Herber Curtis (USA, Lick)
use photography

36" Crossley reflector @ Lick : [image]
estimates ~120,000 nebulae accessible; ~50% are spiral
- 1906-22 : Jacobus Kapteyn (Dutch) :
detailed study of MW : [image]
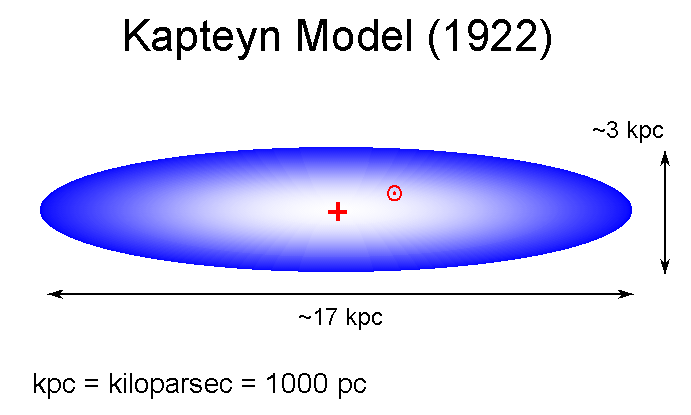
surveys 200 areas : star counts, proper motions, radial velocities
concludes : MW = thick disk, 5kpc radius, sun @ center
considers absorption and finds some reddening, but
assumes Rayleigh scattering so infers (wrongly) absorption unimportant
- 1912 : Henrietta Leavitt (USA, Harvard) :
[image]

Period-Lumimosity relation for Cepheids in Magellanic Clouds
tool for measuring distances
- 1914 : Vesto Slipher (USA, Lowell) : [image]

spectra of spirals (take 80 hours!)
finds large velocities (eg M31 is -300 km/s)
much larger than any MW stars
- 1918 : Harlow Shapley (USA, Princeton/Harvard) : [image]
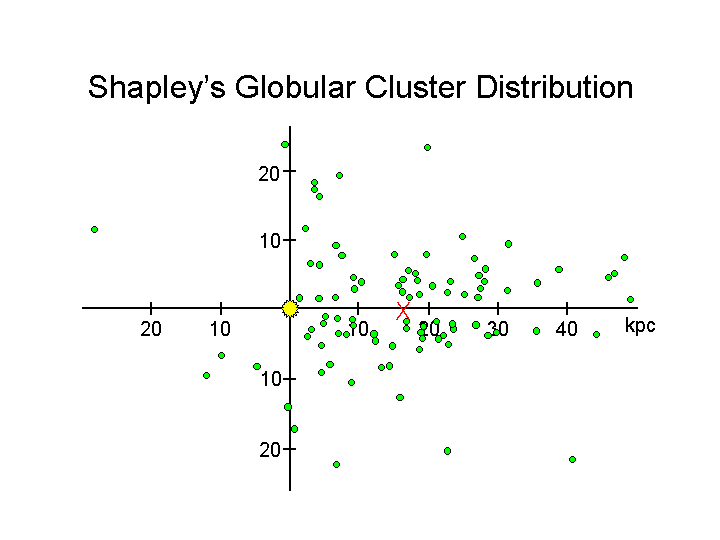
uses Globular Clusters (GCs) to infer "Big Galaxy"
diameter 100 kpc, sun ~15 kpc off-center
10 x Kapteyn's galaxy; suggests absorption was the problem
- 1920 : Shapley (no) - Curtis (yes) Debate
: "Are Spiral Nebulae Island Universes" [image]
public debate @ National Acadamy of Science, Washington DC.
 Short (30min) presentations, but summary articles published 1921
Short (30min) presentations, but summary articles published 1921
surprisingly, Shapley "won" the debate, though Curtis was right.
Shapley :
new MW so big, inconceivable universe so much bigger
van Maanen rotation rules out distant spirals
Curtis :
doubted Shapley's MW size
range in size (0.01-2 deg)
 range in distance (1000x more than MW)
range in distance (1000x more than MW)
Novae in M31  100 kpc away and size of Kapteyn's MW
100 kpc away and size of Kapteyn's MW
spectra show large doppler shifts, yet no proper motions
some edge on spirals have dust lanes  similar
to MW (zone of avoidance)
similar
to MW (zone of avoidance)  external
external
- 1923 : Edwin Hubble (USA, Mt Wilson) :
uses the new 100" [image]

finds Cepheids in M31  300 kpc (now, 770 kpc)
300 kpc (now, 770 kpc)
 external galaxy
external galaxy
(centennial review of Hubble's career by Sandage :
[ o-link ])
(d) 1925 - 1950 : Expanding Horizons
- 1927 : Bertil Lindblad (Sweedish) and Jan Oort (Dutch) : [image]


Lindblad predicts differential rotation near sun; Oort find it
supports Shapley's MW with sun off-center (against Kapteyn's MW)
however, derives smaller size than Shapley
- 1929 : Edwin Hubble and Milton Humason (USA, Mt Wilson)
[image]

Finds redshift-distance relation (Hubble's Law) (Original paper:
[ o-link ])
already expected from de Sitter's solutions to GR
looked for by others; Hubble used distance ladder, including Cepheids
1931 - includes many more galaxies
H ~ 530 km/s/Mpc  2 Gyr age
(less than earth !?)
2 Gyr age
(less than earth !?)
- 1930 : Robert Trumpler (USA, Lick) :
compares sizes and CM diagrams of open clusters
concludes absorption pervasive (~0.5mag/kpc, close to correct)
nail in the coffin of Kapteyn's Milky Way
- 1936 : Hubble : publishes galaxy classification (tuning fork) [image]
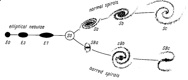
uses names (early, late) influenced by Jean's theory of gravitational collapse
eg E's = large gas cloud, evolves into spiral
- 1930s : Fritz Zwicky (Swiss/USA, Cal Tech) :
[image]

measures galaxy velocities in Coma;
infers dark matter needed if clusters are bound
no one believes him
- 1944 : Walter Baade (German/USA, Mt Wilson) : [image]

observes Spiral bulges & Ellipticals (war time black-outs help)
uncovers stellar populations :
- Pop I : blue supergiants in disks
- Pop II : red giants in bulges and Ellipticals
(e) 1950 - Present : Modern Developments
- 1952 : Baade : uses 200" to recalibrate
Cepheid P-L relation
depends on Pop I or II; previous work used wrong relation
 all distances doubled
all distances doubled
 M31 is similar in size to MW
M31 is similar in size to MW
 Universe doubles in size (!)
Universe doubles in size (!)
- 1962 : Eggen, Lynden-Bell & Sandage (ELS) : [image]

Collapse model for formation of MW galaxy
Accounts for position/kinematic/metallicity gradients
Importance of ELS picture still debated
- 1963 : Maartin Schmidt (German/USA, Cal Tech) : [image]
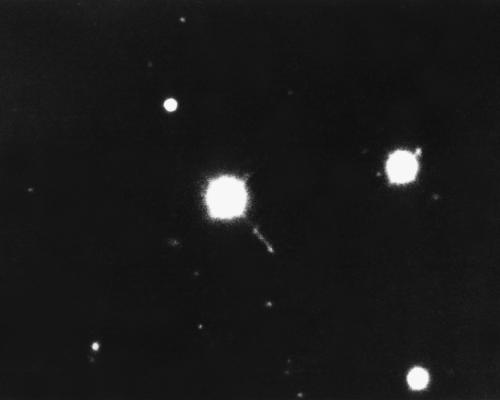
Discovers Quasars (identifies redshift of 3C 273).
- 1965 : Arno Penzias & Robert Wilson (USA, Bell Labs) : [image]

Discover Cosmic Microwave Background (CMB)
Strong support for Hot Big Bang model
- 1972 : Leonard Searle & Wal Sargent (USA, Cal Tech) :
measure 24% He basiline in low metallicity Dwarfs
consistent with Big Bang nucleosynthesis
- 1970s : Vera Rubin et al. (USA, Carnegie) : [image]

infers dark matter from spiral rotation curves
inspires Cold Dark Matter (CDM) models of 80s-90s
- 1978 : Len Searle & Robert Zinn (USA, Cal Tech) :
Abundance analysis of MW Globular Clusters: infer range of ages
Suggest MW halo built up by accretion of fragments after main formation
- 1980 : Alan Guth & Alexei Starobinski (USA; USSR) : [image]

Independently conceive of early period of extremely rapid, accelerated expansion.
Guth calls this "inflation": solves several deep problems.
Provides natural explanation for creation of everything, and launching the expansion.
- 1992 : COBE (NASA): [image]

measures stunningly accurate black body spectrum
finds slight (10-5) anisotropies in CMB
 pregalactic structure
pregalactic structure
- 1996 : HST's HDF (NASA): [image]

galaxies down to 29m; out to z~3; total ~1010
young galaxies visibly different
early star formation rate is high ("Madau" plot)
- 1998 : High-z SN Projects (USA, Berkeley & Harvard): [image]
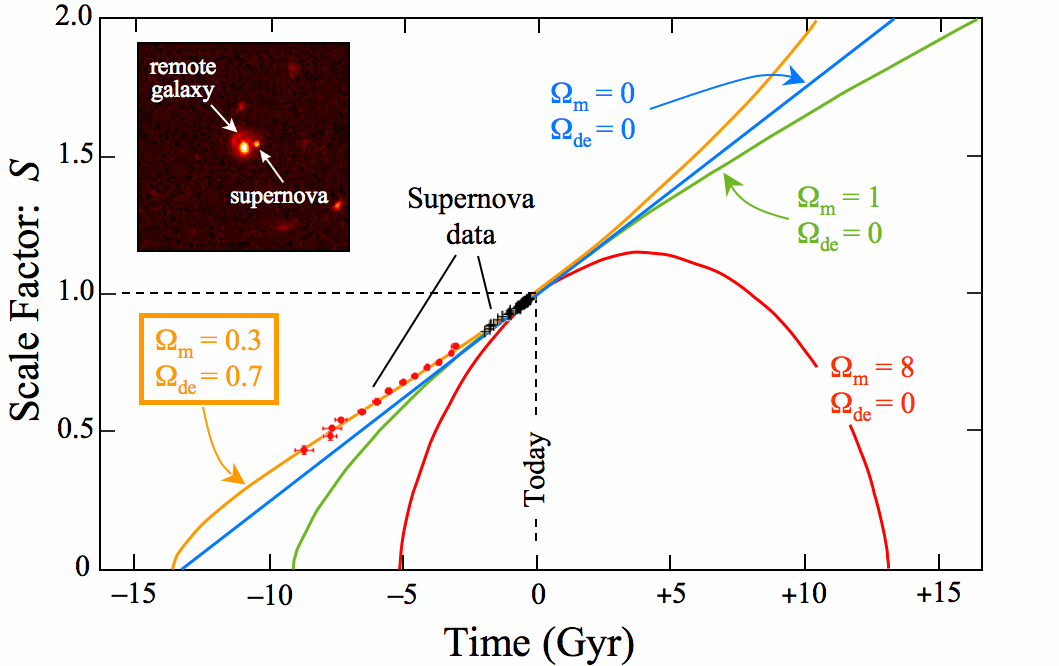
Two groups use Type Ia SN as standard candles out to z ~ 1
Both find evidence for non-zero cosmological constant (universe
accelerating)
- 2003 : 2dF (& SDSS) Galaxy Surveys (UK/Australia & USA): [image]
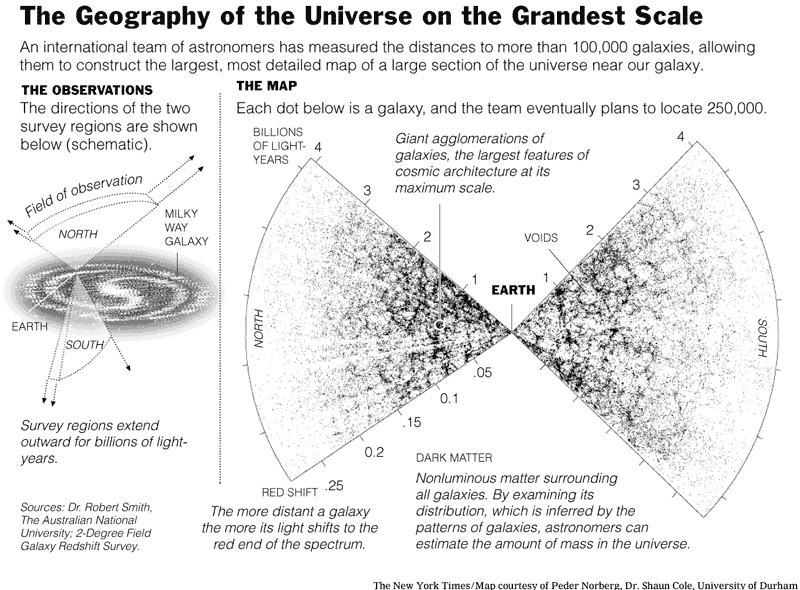
The first of the large scale galaxy redshift surveys is completed (2dF)
250,000 galaxy redshifts out to z~0.1 allow detailed analysis of large scale structure.
SDSS completed later (800,000 galaxy redshifts) but with more detailed information.
- 2003 : WMAP (NASA) : [image]
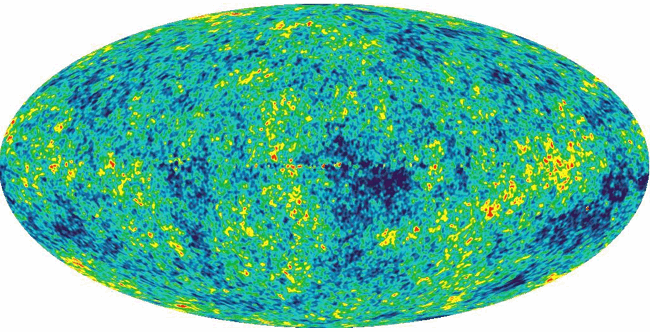
CMB power spectrum measured; includes accoustic peaks 1,2,(~3)
inspires concordance model with "high" accuracy (few %)
combines : WMAP; SN-1a; 2dFGRS; HST-Ho;
BBNS; to find : [image]
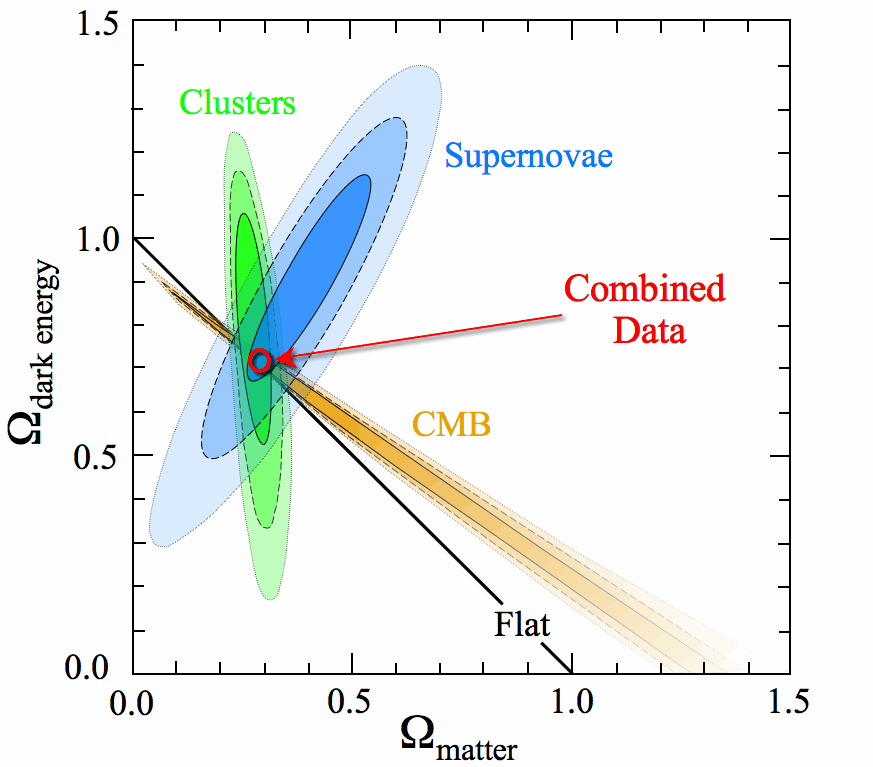
- flat geometry
- 70% Dark Energy; 26% Dark Matter; 4% Baryonic Matter
- age 13.7 Gyr
- initial fluctuation spectrum is power law, index -1 (consistent with inflation)



(3) Preliminaries
Before delving into the subject proper, there are a few preliminaries worth introducing.
(a) Basic Scales
The following ASTRO-101 type diagrams remind us of the relative size of galaxies and our visible horizon
-
Remind yourself, using simple scale models, just how BIG the Universe is: [image].
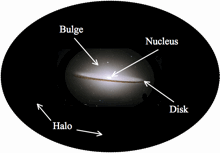
(b) Galaxies are Multicomponent Systems
- Three constituents, with rough mass ratio 1/10/100 : Gas / Stars / Dark Matter
The first two have complex identity :
- Gas: different phases; dynamics; composition; (like "weather")
- Stars: different ages; locations; kinematics; metallicities; (like "cars")
The third is simpler but more enigmatic:
- DM: collisionless "gas" (of WIMPs?); huge; ~smooth; centrally concentrated
- Several components, with varying prominence depending on galaxy type
[image].
(c) Colors and Spectra

- A montage of SDSS galaxies shows a limited range of colors: blue -- red [image]
Statistical analysis suggests the color distribution is roughly bimodal [image].
Crudely speaking:
blue = younger population
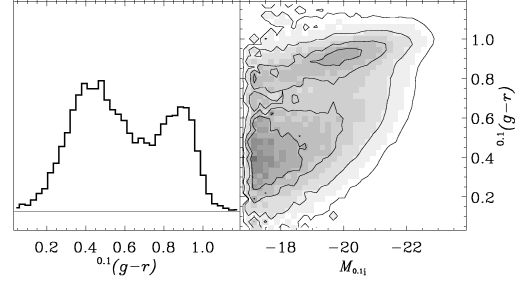
red = older population (actually, more like yellow/orange)
- This can be understood in terms of stellar evolution:
Following an episode of star formation, the main sequence "erodes" downwards.
[image].
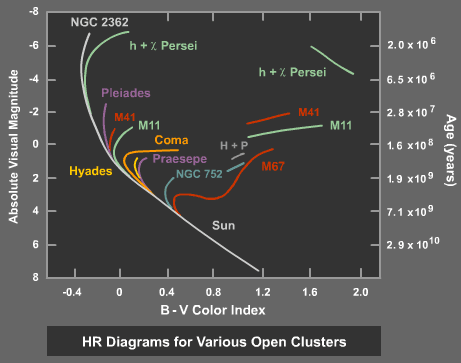
Young population: light is dominated by higher mass main sequence stars.
Older population: light is dominated by red giants.
(In both cases these are a minor but luminous sub-population.)
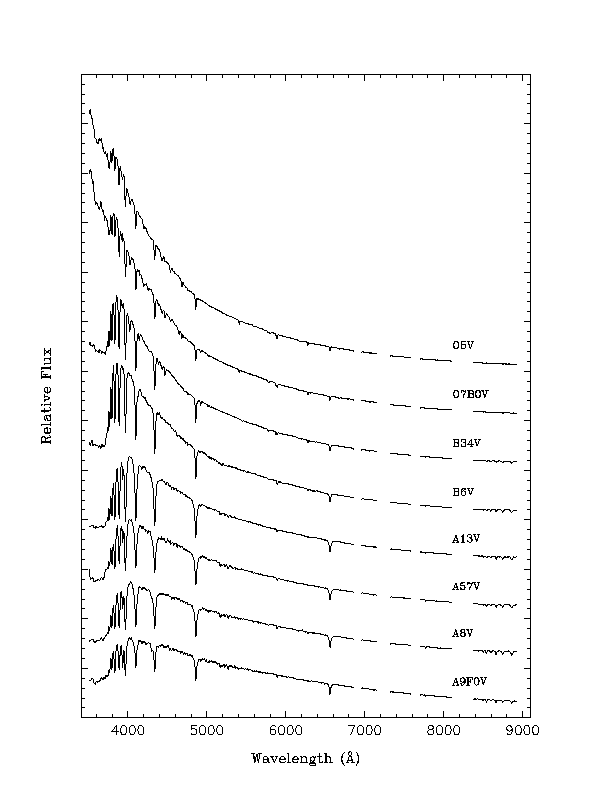
- Spectra show in more detail these population differences
Star spectra primarily follow the spectral type [image].
Galaxy spectra show mixed populations [image].
- Analysis of these spectra can reveal many properties:
- population mix of stars
- current star formation (e.g. emission lines)
- metallicity (fraction of heavy elements, i.e. beyond He)
- kinematics of gas and stars: rotation and dispersion.
(d) Useful Units
Calculations of galaxy properties are greatly simplified with sensible units
(see also: Toolbox).
Rather than "mks" or "cgs" for length/mass/time, we can use:
"psm" : parsec, solar mass, Megayear : pc, M , Myr , Myr
|
There are a number of nice features to this system:
- (1) Velocity in psm units, pc/Myr, is the same as km/s (within 2%; 1pc/Myr = 0.9778 km/s)
(recall the pnemonic: "a kilometer per second is a parsec in a million years ")
- (2) Newton's constant: G = 4.50 × 10-3 (4.49846 × 10-3)
its units are: (pc3/M ) Myr-2
) Myr-2

 -1 Myr-2
-1 Myr-2  (km/s)2 pc M
(km/s)2 pc M -1
-1
- (3) Equations, such as M = R V2 / G, directly accept and yield observational values
- (4) Densities,
 psm, are in M
psm, are in M /pc-3 = 6.76 × 10-23 gm cm-3 = 40.4 mp cm-3 = 3.60 × 106 h2
/pc-3 = 6.76 × 10-23 gm cm-3 = 40.4 mp cm-3 = 3.60 × 106 h2 crit
crit
- (5) Frequencies, Myr-1, are also velocity gradients: km/s/pc
- (6) Crossing/collapse times: R(pc) / V(km/s) = 1 / (G
 )½ are in Myr.
)½ are in Myr.
Some examples illustrate psm units, and introduce basic galaxy properties :
(see homework for further examples).
There are a few extensions to the psm system which can, at times, be useful:
- psm energy units: peu (M
 pc2Myr-2) = 1.89 × 1036 Joules
pc2Myr-2) = 1.89 × 1036 Joules
- psm luminosity units: plu (peu/Myr) = 5.97 × 1022 Watt = 1.56 × 10-4 L

- mass/luminosity units: M
 /plu = 3.33 × 107 kg/Watt = 6400 (M
/plu = 3.33 × 107 kg/Watt = 6400 (M /L
/L )
)
- linear momentum: pmu (M
 pc/Myr
pc/Myr  M
M km/s) = 1.85 × 1033 kg m s-1
km/s) = 1.85 × 1033 kg m s-1
- angular momentum: pamu (M
 pc2Myr-1
pc2Myr-1  M
M km/s pc) = 5.71 × 1049 kg m2 s-1
km/s pc) = 5.71 × 1049 kg m2 s-1
- force (momentum flux): pfu (M
 pc/Myr2
pc/Myr2  M
M km/s/Myr) = 5.86 × 1019 N
km/s/Myr) = 5.86 × 1019 N
- acceleration: pau (pc/Myr2
 km/s Myr-1) = 3.09 × 10-11 m s-2
km/s Myr-1) = 3.09 × 10-11 m s-2
A few more examples help illustrate:
(e) Magnitude Systems and Surface Brightness
The previous section deals only with dynamical variables : V, R, t, M.
Let's introduce starlight into the mix, not least because it is easy to measure.
Astronomers use two systems: magnitudes and fluxes (each with apparent and intrinsic)
it can sometimes be tricky jumping back and forth between these systems.
- Magnitudes:
The generic magnitude is defined:
where flux_0 is a reference flux for a star with m = 0.0 (usually Vega), and is filter-specific.
Typically, m ~ 12 - 14 (nearby galaxies); 16 - 18 (distant galaxies); 21 - 25 (very distant galaxies).
Apparent magnitudes, m, include information on both intrinsic luminosity and distance.
Absolute magnitude (M) is defined as the apparent magnitude (m) were the object at 10pc, i.e.:
m = const - 2.5 log fd pc
M = const - 2.5 log f10pc
but from the inverse square law:
f10pc = fd pc × (dpc / 10)2
so, substituting:
M = const - 2.5 log [fd pc × (dpc / 10)2]
M = const - 2.5 log fd pc - 2.5 log dpc2 - 2.5 log (1/100)
Giving the well-known relation:
By placing everything at 10pc, absolute magnitudes are related to an object's luminosity
M ~ -10 to -17 (dwarfs);
M ~ -18 to -21 (normal galaxies);
M ~ -22 to -24 (giant galaxies & QSOs).
- Solar magnitudes and fluxes:
Often, we express luminosities relative to the sun (e.g. 3 × 108 LV, )
)
The sun's absolute magnitude in band X = U,B,V,R,I is MX, =
5.66, 5.47, 4.82, 4.28, 3.94.
=
5.66, 5.47, 4.82, 4.28, 3.94.
Hence, an object with absolute magnitude MX, has luminosity:
- Surface Brightness:
Extended objects have surface brightness, µ in mag arcsec-2 (mag/ss; sometimes written 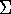 )
)
Since µ is independent of distance it immediately gives the surface
luminosity density, I L pc-2
pc-2
e.g. using M ,B from above, we find (see homework) :
,B from above, we find (see homework) :
and in general, for U,B,V,R,I, the constant is: 27.23, 27.04, 26.39, 25.85, 25.51.
- Example:
M87 has a central surface brightness µV = 17 mag/ss.
 the core has projected luminosity density: IV = dex[ -0.4(17 - 26.39)] = 5,700 LV,
the core has projected luminosity density: IV = dex[ -0.4(17 - 26.39)] = 5,700 LV, pc-2.
pc-2.
if the core radius is 10 arcsec, what's the core's apparent magnitude?
 mcore ~ 17 - 2.5 log [
mcore ~ 17 - 2.5 log [ ×102] = 10.75
×102] = 10.75
for a distance of 15 Mpc, what's the total core luminosity?
 M = m - 5log dpc + 5 = -20.13, giving L = dex[-0.4(-20.13 - 4.82)] = 9.55 × 109 LV,
M = m - 5log dpc + 5 = -20.13, giving L = dex[-0.4(-20.13 - 4.82)] = 9.55 × 109 LV,
Using 10 arcsec = 10 × 15 × 106/206265 = 730 pc, we find a luminosity density:
 jcore ~ Icore / 2 rcore ~ 3.9 LV,
jcore ~ Icore / 2 rcore ~ 3.9 LV, pc-3.
pc-3.
to find the mass density requires a mass-to-light ratio, which is our next topic:
(f) Mass to Light Ratios
Light and dynamics are coupled using "Mass to Light Ratios (M/L)".
- "Mass to Light" (M/L) ratios are important for two reasons :
- they allow us to estimate mass (important but difficult to measure)
using light (easy to measure)
- they tell us about the content of a system,
eg (M/L) values differ : pop I < pop II < galaxy+halo < clusters
- Solar units are used : where (M/L)

 M
M /L
/L
 1
1
Physical units : kg/Watt are not generally used
[conversion: (M/L) ,bol = 5173 kg/Watt = 0.5173 gm/(erg/s) ]
,bol = 5173 kg/Watt = 0.5173 gm/(erg/s) ]
(M/L) is expressed at a given waveband, most commonly B,V,I,K, or bolometric (all  ).
).
e.g. for waveband "X", using absolute magnitudes :
(M/L)X = M/M /
LX/L /
LX/L ,X = M/M ,X = M/M / dex[ -0.4( MX - M
/ dex[ -0.4( MX - M ,X) ] ,X) ]
|
| 1.5 |
where MX & M X are X-band absolute magnitudes of the object & sun;
X are X-band absolute magnitudes of the object & sun;
and LX & L X are X-band luminosities of the object & sun
X are X-band luminosities of the object & sun
and X = U,B,V,R,I,K,bol and M X =
5.66, 5.47, 4.82, 4.28, 3.94, 3.33, 4.74
X =
5.66, 5.47, 4.82, 4.28, 3.94, 3.33, 4.74
note : (M/L)X is the same for all X only if the object and sun
have the same colors
(careful: M used for both mass and absolute magnitude here - sorry)
One can also use luminosities (usually only bolometric)
L ,bol = 3.84 x 1033
erg s-1 and Mbol =
-2.5 log(Lbol / L
,bol = 3.84 x 1033
erg s-1 and Mbol =
-2.5 log(Lbol / L ,bol) + 4.74
,bol) + 4.74
- For main sequence stars, we have L
 M3.5, giving :
(M/L)
M3.5, giving :
(M/L)  M-2.5
M-2.5  L-0.71
L-0.71
showing, as one expects, later spectral types have higher M/L.
eg K stars : M ~ 0.5M
 M/L ~ 10; A stars : M ~ 2.0M
M/L ~ 10; A stars : M ~ 2.0M
 M/L ~ 0.1
M/L ~ 0.1
- For composite systems, M/L reflects the average M/L over the population
- Pop I (young) : massive stars dominate light; low mass stars dominate mass
- Pop II (old) : giants dominate light; M.S. stars dominate mass
 Typical galaxy (& solar neighborhood) has M/LV ~ 6 , M/LB ~ 10
Typical galaxy (& solar neighborhood) has M/LV ~ 6 , M/LB ~ 10
 In general : M/L increases with age and metallicity
In general : M/L increases with age and metallicity
 Maximum range : 2 < M/LB < 20.
Maximum range : 2 < M/LB < 20.
Dark components further increase these values, eg
- SMBH in galaxy nuclei
- Dark Matter in galaxy halos
More specifically, for main sequence stars and composite systems in V :
| Type |
M / M |
MV |
LV / L ,V ,V | (M/L)V |
| O5 | 60 | -5.7 | 16,140 | 0.0037 |
| B5 | 5.9 | -1.2 | 255 | 0.023 |
| A5 | 2.0 | +1.95 | 14 | 0.14 |
| F5 | 1.4 | +3.5 | 3.4 | 0.41 |
| G5 | 0.92 | +5.1 | 0.77 | 1.19 |
| K5 | 0.67 | +6.4 | 0.23 | 2.87 |
| M5 | 0.21 | +12.3 | 0.001 | 206 |
|
| System |
(M/L)V |
Reason |
| HII region | 0.3 - 1 | Pop I only |
| Spiral Disk | 2 - 5 | Pop I + II |
| Bulges / Ellipticals | 8 - 15 | Pop II |
| Nucleus (no AGN) | 10 - 50 | BH present |
| Galaxy + halo | 20 - 50 | DM important |
| Clusters | 100 - 500 | DM dominates |
| Universe | ~1000 | DM dominates |
|
(g) Cosmology 101
- The Hubble Law
The most basic piece of cosmology is the Hubble Law, which arises from Cosmic expansion.
where v is recession velocity, d is distance, and H0 is Hubble's constant ~ 72 kms/s/Mpc
Example: what's the distance to a galaxy with z = 0.02?
v  cz = 6000 km/s,
cz = 6000 km/s,
so d = v / H0 = 6000 / 72 = 83.3 Mpc = 272 Mly
This now allows you to calculate luminosities & linear sizes from fluxes & angular sizes.
Note: at higher z (e.g. > 0.3), this equation won't work, and one needs a more sophisticated approach.
Also, at very low z, peculiar velocities can be significant introduce errors to distances.
- Use of Scaled Hubble Constant: h
For decades, Ho was uncertain to ~50%
It was/is useful, therefore, to set Ho to 100h km/s/Mpc with
h kept explicit
h appears once for each redshift-distance, with a power of opposite sign: e.g.
Note that h does not appear for non-redshift distances (eg
Cepheid distances).
Although we now know h=0.72 (with ~5% uncertainty), its good to
keep using it.
- Concordance Model Parameters
After WMAP, the various cosmological datasets have yielded a robust cosmological model.
The total density is equal to the critical density ( tot = 1.00) so the spatial geometry is Euclidean.
tot = 1.00) so the spatial geometry is Euclidean.
The breakdown of today's densities is:  b = 0.04,
b = 0.04,  dm = 0.23,
dm = 0.23,  de = 0.73,
de = 0.73,  r = 8.4 × 10-5.
r = 8.4 × 10-5.
 These are routinely used to define the relation between redshift and other important parameters, including cosmic time [image]
These are routinely used to define the relation between redshift and other important parameters, including cosmic time [image]
- Intermediate & High Redshift
It is now routine to ask how any properties change with redshift (i.e. cosmic epoch)
It is therefore useful to have a basic feel for the link between z and lookback time.
- z ~ 1 is ~60% lookback time (LBT), with cosmic age ~6 Gyr
- coasting (changover from de to ac-celeration) occurs at z~0.65 or ~45% LBT
- high-z galaxies and QSOs at z~4-6 are at ~90% LBT, age ~1Gyr
- recombination is at z=1100, T=3300K, age=380 kyr,
 ~103 cm-3
~103 cm-3
- at recombination, 10kpc subtends ~2.8 arcmin, or 1 deg ~170 kpc
- matter/energy equality occurs at z~3300, T~10,000K, age~50 kyr.
This concludes our introduction to the subject of Extragalactic Astronomy
We are now ready to start, relatively gently, with Topic 2 : Galaxy
Morphology.






 30 yrs is a golden time.
30 yrs is a golden time.
 currently fertile area (astronomy
is prominent amongst physical sciences)
currently fertile area (astronomy
is prominent amongst physical sciences) 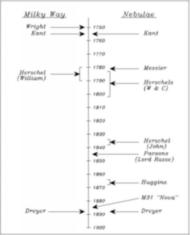








































 , Myr
, Myr

 -1 Myr-2
-1 Myr-2  (km/s)2 pc M
(km/s)2 pc M )
) ×102] = 10.75
×102] = 10.75  ).
).
 M3.5, giving :
(M/L)
M3.5, giving :
(M/L)  tot = 1.00) so the spatial geometry is Euclidean.
tot = 1.00) so the spatial geometry is Euclidean.