Whittle : EXTRAGALACTIC ASTRONOMY




9. GAS & DUST IN GALAXIES
Under Current Construction
: last update feb 20 2005


(1) Galaxy ISMs : An Overview
- Like the Earth, galaxies have an atmosphere
 a gaseous component held "down" by gravity
a gaseous component held "down" by gravity
this atmosphere fills the space between stars, hence: interstellar medium (ISM)
by mass, the ISM is usually not very important: MISM  1% Mstars
1% Mstars
The average midplane density is ~1 cm-3  columns ~3×1021cm-2/kpc (~0.005 gm cm-2/kpc)
columns ~3×1021cm-2/kpc (~0.005 gm cm-2/kpc)
 galaxy disks have "thickness"
galaxy disks have "thickness"  5 cm of Earth's atmosphere (~1 meter of air to the GC).
5 cm of Earth's atmosphere (~1 meter of air to the GC).
- The ISM contains: starlight; gas; dust; cosmic rays; magnetic fields
Near the sun they all have similar energy density  pressure
pressure  1 eV cm-3
1 eV cm-3
- The element mix is the usual: H/He/others: 74/24/2 (% by mass); 90/10/0.01 (% by number)
Of the "others", ~10-50% have condensed out as solid particles: "dust".
- Despite its low mass, the ISM is ultimately very important, for several reasons:
- It plays a crucial role in the star
 gas cycle
gas cycle
- in spirals and irregulars, it facilitates ongoing (& current) star formation
- it is a repository for element buildup and is therefore integral to chemical evolution
- Because it can cool, its collapse is dissipational
- stars can form !! hot gas
 cold gas
cold gas  stars
stars
- new generations of stars "cool" spiral disks, allowing arm formation
- globally, gas can migrate inwards to smaller radii:
 galaxies are smaller than dark matter halos !
galaxies are smaller than dark matter halos !
 galaxies have steep density gradients
galaxies have steep density gradients
 galaxy nuclei can have very high densities, including an SMBH
galaxy nuclei can have very high densities, including an SMBH
- Being atomic/molecular, its emission & absorption provides enormous diagnostic information
Some examples :
- Doppler motions reveal galaxy dynamics
- abundance measurements allow study of chemical evolution
- physical conditions: density; temp; pressure; turbulence; columns; mass, can all be derived
- some emission lines can be seen (relatively) easily at cosmological distances.
- high redshift QSO absorption lines reveal halo & disk evolution.
- The ISM can dominate a galaxy's integrated SED (spectral energy distribution):
starlight dominates the UV-NIR; but the ISM dominates outside this range.
- Mid-IR to Sub-mm is dominated by emission from dust
- Soft X-rays come from the hot ISM phase (though X ray binares can be important)
- cm-radio comes either from HII regions or a relativistic magnetoionic plasma
- certain emission lines (eg Ly
 ; [CII]
; [CII] 158µ) can be major coolants
158µ) can be major coolants
- The ISM is energized primarily by stars (starlight, winds, supernovae)
 UV starlight photoionizes atoms & dissociates molecules; photo-ejected electrons heat gas
UV starlight photoionizes atoms & dissociates molecules; photo-ejected electrons heat gas
 SN shocks heat/ionize/accelerate gas & are largely responsible for the ISM's complexity.
SN shocks heat/ionize/accelerate gas & are largely responsible for the ISM's complexity.
- The ISM can be highly inhomogeneous, with several phases
These phases are (roughly): hot/warm/cold, with low/medium/high density
In a wide range of conditions these phases have similar pressures
 P/k
P/k  nT
nT  104
104  1 eV cm-3.
1 eV cm-3.
However, in dynamic situations, pressure balance is no longer applicable.
The ISM contains cloud and intercloud components with density contrast ~ 102-105
 these clouds are not like terrestrial clouds; more like blocks of wood or lead hanging in the air.
these clouds are not like terrestrial clouds; more like blocks of wood or lead hanging in the air.
- The ISM is a dynamic environment, with mass exchange between phases
- cooling facilitates: hot
 warm
warm  cold
cold  stars.
stars.
- supernovae inject energy which accelerates the gas and continuously rearranges the geometry
 e.g. a disk ISM will "boil" & "bubble" with gas cycling out & back above the disk.
e.g. a disk ISM will "boil" & "bubble" with gas cycling out & back above the disk.
- sporadically, tidal encounters & their resulting starbursts can:
- add fresh (low metallicity) gas
- energize and evacuate large regions
- cycle gas into the halo, some of which may return later.
- radically alter the ISM, e.g. spiral + spiral
 elliptical.
elliptical.
As always, our current view is just one frame of a long and intricate movie.
- What about the distribution of ISM (particularly in spiral disks)?
- Globally the scale height depends on the phase's temperature/velocity dispersion and
 colder phases are confined closer to the plane
colder phases are confined closer to the plane
 hotter &/or more turbulent phases are thicker
hotter &/or more turbulent phases are thicker
 in disks, the ISM flares at large radii and is thinner at small radii).
in disks, the ISM flares at large radii and is thinner at small radii).
However, high local energy density can affect this distribution by driving vertical blow-out.
- Locally: the ISM is highly complex & "foamy"
SN evacuate complex interconnected "superbubbles"
between are sheets & clouds of denser colder gas.
- The Milky Way can act as a template for studying other galaxy ISMs
As usual, the proximity of the MW's ISM offers important insights
Hence, MW ISM studies are now extensive & comprise a major area within astronomy
Here, we consider only the bare essentials, providing a framework for discussing ISM in other galaxies.



(2) ISM Components & Their Observational Signatures
(a) Introduction
While ultimately ISM gas spans all conditions, in practice much resides in one of several components
These components are distinguished by their phase (n,T,Xe) and their
location
This figure and the following table summarize the major components:
| Component |
Temp
K |
Density
midplane
cm-3 |
Pressure
nT
K cm-3 |
Xe
ionization |
FF
filling
% |
<h>
thickness
pc |
| Intercloud |
| Hot HII (HIM) |
106 |
0.002 |
2000 |
1 |
50: |
3000: |
| Warm HII (WIM) |
8000 |
0.15 |
1200 |
1 |
20 |
1000 |
| Warm HI (WNM) |
8000 |
0.3: |
2400 |
0.5 |
30: |
500 |
| Clouds |
| Cold HI (CNM) |
120 |
25 |
3000 |
0.1 |
2 |
100 |
| Cold H2 (CNM) |
15 |
200 |
3000 |
10-4 |
0.1 |
75 |
Note that overall, the intercloud/cloud fraction by mass is ~50 : 50 but by volume it is ~98 : 2
- Three other important components add to the mix :
- Dust: 1nm - 1µm solid particles are found in essentially all phases
~50% heavy elements are in dust (~100% of the refractories)
Dust is discussed more in section 8 (link)
- Magnetic fields: generally a few µGauss in both ordered and random components
energy density: B2/8
 10-12 erg cm-3
10-12 erg cm-3  1 eV cm-3
1 eV cm-3
field compression in superbubble expansion effects on ISM structure (see below).
- Cosmic Rays: relativistic electrons & protons, created in SN shocks
these diffuse throughout the galaxy and permeate all phases (some even hit the earth)
they are a primary heating source in DMC cores (which are otherwise shielded).
the most energetic electrons + magnetic fields  radio synchrotron
radio synchrotron
proton collisions with nuclei  diffuse gamma emission
diffuse gamma emission
equipartition with B field likely, so suspect ~1 eV cm-3
(b) Observational Signatures: General Considerations
All observations involve either emission or absorption
these, in turn, depend on Emission Measure (EM) and column density (N)
- Emission processes are usually collisional, so are
 n2
n2
surface brightness is therefore 
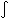 <n2> dl pc cm-6
<n2> dl pc cm-6  Emission Measure (EM).
Emission Measure (EM).
- Absorption processes, in contrast, are

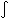 <n> dl cm-2
<n> dl cm-2  Column Density (N).
Column Density (N).
- For ionized gas, the relevant density is usually ne
The table shows EM & Ne for various systems:
| Medium |
ne
cm-3 |
Size
pc |
EM
pc cm-6 |
Emission
Visibility |
Ne
cm-2 |
Absorption
Visibility |
| Young Nova |
107 |
10-3 |
1011 |
v. bright! |
3 ×1022 |
thick |
| PN |
104 |
10-1 |
107 |
bright |
3 ×1021 |
good |
| HII Region |
10 |
102 |
104 |
fine |
3 ×1021 |
good |
| Diffuse ISM |
10-1 |
103 |
10 |
difficult |
3 ×1020 |
good |
| Halo |
10-3 |
104 |
10-2 |
invisible |
3 ×1019 |
fine |
Note, for a typical crossection ~ aBohr ~ 10-16 cm-2, N ~ 1014 cm-2 gives  ~ 1%
~ 1%
This is easily measurable with suitable background source
 low density gas invisible in emission can often be studied in absorption.
low density gas invisible in emission can often be studied in absorption.
- Photoioniztion thresholds render the ISM highly opaque in the EUV:
ionization potentials 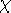 for H, He, He+ are 13.6, 24.6, 54.4 eV (= 91, 50, 25 nm)
for H, He, He+ are 13.6, 24.6, 54.4 eV (= 91, 50, 25 nm)
since  photo
photo  (E-Ei)-3, then:
(E-Ei)-3, then:
- the ISM is highly opaque in EUV (13.6 - 100 eV)
- it is becoming transparent in soft X-ray (~0.6 keV)
- it is completely transparent by 2 keV.
- A wide range of
 E transitions yield features at many wavelengths:
E transitions yield features at many wavelengths:
Transition  E E
eV |
wavelength
range |
Cause |
| 10-6 |
21 cm |
electron spin flip in atomic H |
| 10-2 - 10-3 |
FIR - mm |
molecular rotation |
| 0.1 - 0.01 |
NIR - FIR |
gas molecular vibration;
bond bending in dust |
| 0.03 - 0.003 |
MIR - sub-mm |
phonons in dust @ T ~ 1000-10 K |
| 1 - 10 |
UV - NIR |
outer shell electron transitions
in atoms and molecules |
| 10 - 103 |
EUV - X-ray |
inner shell electron transition;
50 - 500 km s-1 post shock gas |
Note some useful conversions: EeV  1240/
1240/ nm
nm  TK / 7740 per particle.
TK / 7740 per particle.
so @ T 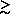 105K, H & He are fully ionized, and
kT ~ EUV - soft X-ray
105K, H & He are fully ionized, and
kT ~ EUV - soft X-ray
(c) Warm Ionized Gas
(d) Hot Ionized Gas
(e) Warm & Cold Atomic Gas
(f) Molecular Gas
(g) Dust
(h) Relativistic Component



(3) Theories of the Multi-Phase ISM



(4) Gas in Disk Galaxies



(5) Gas in Elliptical Galaxies



(6) Gas in Galactic Nuclei



(7) Gas in Galaxy Halos



(8) Dust: Particles in the ISM
(a) Overview
- All ISM gas phases are optically transparent (or very nearly)
However, the Milky Way shows patchy obscuration of background starlight (image)
What causes this optical absorption?
 solid particles with size
a
solid particles with size
a 
 light (nm - µm)
light (nm - µm)
Astronomers call these particles "dust", though a better word might be "smoke".
- By human standards, the ISM is exceedingly filthy.
Imagine bringing the ISM
to atmospheric number density (3 × 1019 cm-3)
 it would be a thick smog with ~1 mag/meter [~1 mag/inch at
it would be a thick smog with ~1 mag/meter [~1 mag/inch at
 air] !!
air] !!
 You could not see across a room [your
hand in front of your face] !!
You could not see across a room [your
hand in front of your face] !!
 Walking just a few paces, you'd be covered in an extremely fine black soot.
Walking just a few paces, you'd be covered in an extremely fine black soot.
 This is a chain-smoker's heaven/nightmare: the smoke is rich in carcinogenic PAHs.
This is a chain-smoker's heaven/nightmare: the smoke is rich in carcinogenic PAHs.
- Why is the ISM so dirty ? Because stars are dirty furnaces.
For 10 Gyr they've been "polluting" the ISM by making & blowing off heavy elements
Typically, 10-50% of these elements condense as tiny solid particles: graphite/silicates/ices
 Our atmosphere is clear by comparison because it doesn't contain ~1% particulates.
Our atmosphere is clear by comparison because it doesn't contain ~1% particulates.
- Dust has a huge impact on EM radiation, spanning 3 decades (~1000A - 100µm).
It absorbs UV & optical but is transparent in the IR (grains have size ~ UV).
UV).
 important contributions have come from Copernicus, IUE, HST.
important contributions have come from Copernicus, IUE, HST.
It emits in the IR (since its equilibrium temperature is ~10-100K)
 important contributions have come from IRAS, COBE, ISO, Spitzer.
important contributions have come from IRAS, COBE, ISO, Spitzer.
(b) Quick estimates of some important dust properties
Let's gain some insights from a simplified, yet useful, treatment.
Assume an ISM metallicity of Z~2% (by mass) of which fd ~ 0.1 is condensed as grains.
Assume all grains have dimension a (~0.1µm) and density  (~1 gm cm-3).
(~1 gm cm-3).
The grains absorb and emit as black bodies modified by efficiencies Qabs( ) and Qem(
) and Qem( )
)
In reality, Qabs ~ 1 in the UV, and Qem << 1 in the IR (see below)
However, for now let's take Qabs = Qem = 1 (perfect black bodies)
(i) H column for significant dust opacity
What hydrogen column has geometrical covering factor 1 in dust particles?
- In terms of the hydrogen column, NH cm-2,
the projected mass density in dust is simply:
Nd  a3 = NH mp Z fd gm cm-2 where Nd cm-2 is the column in dust.
a3 = NH mp Z fd gm cm-2 where Nd cm-2 is the column in dust.
Substituting for Nd, the total geometrical
cross section in dust particles is :
Nd a2 =
(NHmp Z fd)/( a3) × a2
a3) × a2  3 × 10-22 × NHfd (Z/Z
3 × 10-22 × NHfd (Z/Z ) × (
) × ( aµ)-1 cm-2
aµ)-1 cm-2
where  is in gm cm-3, a is in µm, and
Z
is in gm cm-3, a is in µm, and
Z = 0.02 is solar metallicity.
= 0.02 is solar metallicity.
(using a2 is OK here, since the absorption efficiency Qabs ~ 1 in the UV/opt).
- For our fiducials, unit covering factor (Nda2 ~ 1 cm2) occurs for NH ~ 3 × 1021 cm-2
Thus, hydrogen columns ~1021.5 cm-2 mark when dust absorption will
be important.
In fact, this simple estimate is very close to the observed value:
AV  NH / (2 x 1021) mags.
NH / (2 x 1021) mags.
- Using the observed value, paths through the ISM suffer an absorption
AV ~ 1.6 × nH dkpc mags
 Spiral disks are optically thick in the
plane, for which <nH> ~ 1 cm-3
Spiral disks are optically thick in the
plane, for which <nH> ~ 1 cm-3
 However, with NH~1021 cm-2 perpendicular to spiral disks, they are borderline transparent.
However, with NH~1021 cm-2 perpendicular to spiral disks, they are borderline transparent.
 DMCs are extremely opaque, since nH~105 gives
AV~100 mag across 1 pc.
DMCs are extremely opaque, since nH~105 gives
AV~100 mag across 1 pc.
 The hot phase (nH ~ 10-3 cm-3) is tansparent (even without likely dust destruction).
The hot phase (nH ~ 10-3 cm-3) is tansparent (even without likely dust destruction).
(ii) Dust number density
Continuing briefly, the dust particle number density is:
- nd/nH = (mpZfd) / (
 a3) = 3.3×10-14 (Z/Z
a3) = 3.3×10-14 (Z/Z fd) / (
fd) / ( aµ3) = 3.3×10-12 for
a ~0.1µm and fd~0.1
aµ3) = 3.3×10-12 for
a ~0.1µm and fd~0.1
For nH ~ 1 cm-3 (the ISM average) this gives nd ~ 1 per (100m)3;
For nH ~ 106 cm-3 (a DMC core) it is ~1 m-3
 dust particles are few and far between !!
dust particles are few and far between !!
(iii) Dust Temperature
- In the ISM, ambient starlight usually has a much greater energy flux than local particles.
 dust is heated mainly by starlight
dust is heated mainly by starlight
At equilibrium, therefore, starlight heating balances radiative cooling
There are two common geometries:
- For isotropic starlight flux Js erg/s/cm2/sr we have:
4 Js
Js  a2 Qabs
a2 Qabs  4
4 a2
a2  Td4 Qem
Td4 Qem
 Td
Td  (
( Js /
Js /  )1/4
(Qabs/Qem)1/4
)1/4
(Qabs/Qem)1/4
- For a distance d from a point source of luminosity L
 we have:
we have:
L /(4
/(4 d2)
d2)  a2 Qabs
a2 Qabs  4
4 a2
a2  Td4 Qem
Td4 Qem
 Td
Td  (L
(L /16
/16 d2
d2 )1/4 (Qabs/Qem)1/4
)1/4 (Qabs/Qem)1/4
Both are independent of a, and Td applies equally for interstellar asteroids, planets, or people.
[This is not quite true, since both Qs do in fact depend on a].
- Consider dust in the general interstellar radiation field. What is Js?
It is roughly what we witness on a clear moonless night, ~0.002 erg/s/cm2/sr.
For Qabs = Qem = 1  Td
Td  3.2K
3.2K
 interstellar space feels very cold!
interstellar space feels very cold!
This result was first obtained by Eddington in 1926.
- This value is, in fact, too low by about ×5.
The reason is that dust does not behave like a black body
It absorbs UV better than it radiates IR  a "green-house" effect.
a "green-house" effect.
The correction factor, [Qabs(UV)/Qem(IR)]1/4 is discussed below (link).
- Dust embedded in HII regions is exposed to a more intense radiation field.
From 2 we have: Td  0.62 × [ (L
0.62 × [ (L /L
/L ) / dpc2 ]1/4 (Qabs/Qem)1/4 K
) / dpc2 ]1/4 (Qabs/Qem)1/4 K
giving Td ~ 10K for L ~ 105L
~ 105L and
d ~ 1pc (with Qabs = Qem = 1)
and
d ~ 1pc (with Qabs = Qem = 1)
Again, this is a factor of a few too low, but still illustrates just how cold dust usually is.
- Dust never achieves high enough temperature to emit outside the IR because:
it has no internal energy source
it's only energy input is starlight
it can emit with fairly high efficiency, because it is a solid
it behaves as a macroscopic, not quantum, system (with one exception, see below)
above ~1500K it evaporates  it never contributes below the Near-IR
it never contributes below the Near-IR
(iv) Dust Emission Efficiency
- In a typical spiral, MISM
 0.05 Mstars
and Mdust
0.05 Mstars
and Mdust  0.01 MISM giving
Mdust
0.01 MISM giving
Mdust  0.0005 Mstars
0.0005 Mstars
However, within factors of a few, LIR  Lopt and we discover that Ldust
Lopt and we discover that Ldust  Lstars
Lstars
How can such a tiny mass of very cold dust compete with nuclear furnaces 104× more massive?
 dust has a huge surface area to mass ratio
dust has a huge surface area to mass ratio
- Consider the sun: it has 1 M
 , and a surface with area
A
, and a surface with area
A = 1.3 × 1011 cm2, at T
= 1.3 × 1011 cm2, at T ~ 6000K
~ 6000K
Now consider 1 M of ISM with 2% heavy elements in dust
with a ~ 0.1µm and
of ISM with 2% heavy elements in dust
with a ~ 0.1µm and  ~ 1 gm cm-3
~ 1 gm cm-3
That makes 4 × 1046 grains with total surface area 5 × 1037 cm2 ~ 1015 A !!
!!
Per unit area, the dust has vastly lower radiative efficiency:
(Td/T )4 ~ (10/6000)4 ~ 10-11
)4 ~ (10/6000)4 ~ 10-11
Qem(IR) ~ 10-4 relative to black body efficiency (see below)
After integrating over populations of both dust and stars:
 dust is a more efficient radiator than stars, per unit mass
dust is a more efficient radiator than stars, per unit mass
(c) The Importance of Dust
For our purposes, dust is important for least two reasons
- it can significantly affect our view of galaxies :
- it blocks UV and optical, which may need correcting
- its emission may enhance or even dominate a galaxy's IR emission
- it can significantly affect crucial ISM processes:
- it facilitates ISM chemistry (surface catalysis)
- it can alter HII region structure (e.g. via Ly destruction)
destruction)
- it dominates DMC cooling, helping star formation
- it can effectively short circuit the deposition of UV/optical input to the ISM
(absorbing and then reradiating in the FIR; e.g. starbursts & AGN).
(d) The Path Ahead
- The simple estimates in (b) above hide a multitude of details
Specifically, we want to explore:
- the composition of grains and their size distribution
- the life cycle of grains: origin, growth and destruction
- dust's affect on light: its emission and absorption properties
- whether dust properties depend on environment (e.g. different ISM phases)
- dust's contriubution to galaxy SEDs (spectral energy distributions)



(9) Dust: Physical Properties
Ascertaining the properties of dust grains has been remarkably difficult, and is still incomplete.
There are two main reasons for this difficulty:
- They are solids; most astrophysical material is ionic/atomic, with simpler associated physics
- Because they are solids, they have more complex/unclear spectral signatures
Nevertheless, progress has been steady, and the subject is now quite sophisticated.
Here we cover just the basic results.
(a) Dust Composition From ISM Gas Depletion
- If heavy elements reside in dust, they must be missing from the ISM gas.
One can study dust composition by studying gas depletion
Gas phase abundances are measured from interstellar absorption lines in stellar spectra.
- The depletion index is defined logarithmically:
D(X) = log10[N(X)/N(H)]obs - log10[N(X)/N(H)]ISM
where [N(X)/N(H)]ISM is the normal relative abundance of element X (usually taken to be solar).
For example, D(C) = -0.7 means C/H is only 20% of its expected value  80% must be in dust.
80% must be in dust.
- Measurements of diffuse clouds (nH~10-100 cm-3) shows significant total depletion ~50%.
Expressed as a total "metallicity", Zd ~ 0.008 (where Z =0.016)
=0.016)
 ~1% of the ISM is in dust, or equivalently ~50% of ISM metals reside in dust.
~1% of the ISM is in dust, or equivalently ~50% of ISM metals reside in dust.
- However, the depletion varies greatly from element to element.
Specifically, depletions increase with condensation temperature, Tc (see figure).
[Tc(X) is the temperature when 50% of element X is solid, for equilibrium conditions]
e.g. Al, Ca, Ti, Fe, Ni are ~100% depleted, while C, N, O, S, Zn show modest or no depletion.
 dust formation involves condensation/adsorption, & not all elements bind efficiently to dust.
dust formation involves condensation/adsorption, & not all elements bind efficiently to dust.
- Depletions also vary with environment: (see figures)
depletion is less for hotter/turbulent ISM & higher velocity clouds
 harsh environments (eg shocks) destroy dust &/or prevent it growing
harsh environments (eg shocks) destroy dust &/or prevent it growing
depletion increases with ISM gas density, at least for some elements
 higher densities facilitate grain growth via adsoption
higher densities facilitate grain growth via adsoption
- In terms of total mass, depletions give the following overall content for dust:
O: 50% C: 20% Fe: 13% Si: 7% Mg: 6% others: 5%
How they are combined is less clear, though IR spectral features help:
 Silicon is in silicates (XSiO3 pyroxines; XSiO4 olivines), where X is mainly Mg, with some Fe.
Silicon is in silicates (XSiO3 pyroxines; XSiO4 olivines), where X is mainly Mg, with some Fe.
 Carbon is in graphite, Polycyclic Aromatic Hydrocarbons (PAH), and amorphous carbon
Carbon is in graphite, Polycyclic Aromatic Hydrocarbons (PAH), and amorphous carbon
 Fe in metallic iron inclusions
Fe in metallic iron inclusions
(these results do not include the various ices which probably condense onto dust in DMCs)
- The depletion patterns support a dust model with resilient refractory core + transient mantle
The elements Fe, Ti, Ni, Ca are primarily core while Mg and Si can be gained and lost.
- Here's a table which summarizes the various dust populations and their properties:
figure
(b) Dust Creation
(c) Subsequent Growth and Destruction of Grains
(d) Dust Grain Size Distribution
(e) Interaction with Light: Mie Theory
If you assume grains are spheres with uniform refractive index, they yield to classical electrodynamics.
This was first worked out by G. Mie in 1908 (in a different context), and the theory goes by his name.
Being a classical theory, wavelength and grain size enter only as their ratio:
X = 2 a/
a/
Here, we only note a few important results.
- First, recall a general refractive index is complex, m = n - ik, where k
tracks absorption.
Ices are good dielectrics, so k is small and n is roughly independent of wavelength.
Metals have k ~ n and both may vary significantly with wavelength.
- Absorption and scattering efficiences, Qabs Qsca, are expressed relative to geometrical :
e.g. for a particular grain/wavelength/index, Mie theory evaluates (see figure, for m = 1.5 - 0.05i)
Qabs(X,m) = (absorption cross-section) /  a2
a2
Qsca(X,m) = (scattering cross-section) /  a2
a2
which define
extinction efficiency : Qext = Qabs + Qsca
and albedo : Alb = Qsca / Qext
- Scattering can be studied by observing reflection nebulae and the diffuse galactic light.
In the optical and UV, scattering is significant with Alb ~ 0.6
(figure)
 grains have significant dielectric character, consistent with silicates.
grains have significant dielectric character, consistent with silicates.
- The mean scattering angle can reveal grain size:
forward for  << a
<< a  isotropic for
isotropic for  >> a
>> a
Observations suggest :
 significant (~45o) angle in optical, increasing (more isotropic) in UV
significant (~45o) angle in optical, increasing (more isotropic) in UV
 optical scattering grains have a~0.1-0.3µm,
optical scattering grains have a~0.1-0.3µm,
 UV scattering grains are much smaller
UV scattering grains are much smaller
- In the limit of
 << a, Mie theory gives:
(figures)
<< a, Mie theory gives:
(figures)
Qabs = 1 (ie  a2 as expected, independent of wavelength)
a2 as expected, independent of wavelength)
Qsca = 1 (also  a2, from diffraction)
a2, from diffraction)
Qext = Qabs + Qsca = 2, which is double the simple geometrical cross section.
- In the limit of
 >> a (i.e. X = 2
>> a (i.e. X = 2 a/
a/ << 1), Mie theory gives:
<< 1), Mie theory gives:
Qabs  -4 X Im[M]
-4 X Im[M] 
 -1 Im[M] where M = (m2 - 1)/(m2 + 2)
-1 Im[M] where M = (m2 - 1)/(m2 + 2)
Qsca  8/3 X4 |M|2
8/3 X4 |M|2 
 -4
-4
 For pure dielectrics (m real, k = 0) then Qsca = Qext
For pure dielectrics (m real, k = 0) then Qsca = Qext 
 -4 and we recover Rayleigh scattering.
-4 and we recover Rayleigh scattering.
 For some absorption (m complex, k
For some absorption (m complex, k 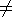 0) then Qext
0) then Qext  Qabs
Qabs 
 -1
-1
which is the correct form for the extinction law in the near, mid and far-IR
 confirming that there are no very large grains (a << 1 - few µm).
confirming that there are no very large grains (a << 1 - few µm).
- Mie theory calculates Qabs(
 ) for absorption, but what about emission: Qem(
) for absorption, but what about emission: Qem( ) ?
) ?
By great good fortune, they are the same !!
 Recall Kirchoff's law: "good (bad) absorbers are good (bad) emitters".
Recall Kirchoff's law: "good (bad) absorbers are good (bad) emitters".
more specifically, for thermal emission:
Fem( ) = Qem(
) = Qem( ) × B
) × B (T) per unit area, where B
(T) per unit area, where B (T) is the Planck function; and
(T) is the Planck function; and
Qem( ) = Qabs(
) = Qabs( ) whose functional form is given above
) whose functional form is given above
(this has its roots in the reversibility of all interactions; a principle called "detailed balance")
- It is now clear that since dust grains don't absorb much in the IR, they will be poor IR emitters
Of course, being good emitters in the UV doesn't help, since BUV(T) is tiny when T ~ few K !
We now have the "green-house" factor:
 Qabs(UV) / Qem(IR)
Qabs(UV) / Qem(IR)  Qabs(UV) / Qabs(IR)
Qabs(UV) / Qabs(IR)
(f) Dust Temperatures
(i) Inferred from IR emission
- First, recall the basic Wein relations for the peak of the Planck function (there are two of them!)
The peak of B d
d is at
is at 
 2900µm/T(K)
2900µm/T(K)
The peak of B d
d is
is 
 2.82kT/h or
2.82kT/h or 
 5000µm/T(K)
5000µm/T(K)
 Often, the difference won't matter.
Often, the difference won't matter.
 Sometimes it does: so check if spectra are in f
Sometimes it does: so check if spectra are in f vs
vs  or f
or f vs
vs  (e.g. Jy vs
(e.g. Jy vs  -1).
-1).
- In fact, since dust's radiative efficiency Qem
 a/
a/ (see below)
(see below)
 even a single Td & single size population doesn't yield a Planck function!
even a single Td & single size population doesn't yield a Planck function!
In reality, a range of Td and grain sizes undermines a straightforward inference of
Td
Nevertheless, emission in NIR (1-5µm) MIR (5-25µm) and FIR (25-300µm) sub-mm (300-1000µm) does indicate clearly different mean values of Td.
- Overall, dust emission can span a broad range, NIR to FIR (sub-mm at higher redshift):
 Td spans a wide range: 1000 - 10K, however ...
Td spans a wide range: 1000 - 10K, however ...
In most galaxies, the bulk is in the FIR, ~60 - 200µm
 the majority of dust has Td ~ 10 - 50K
the majority of dust has Td ~ 10 - 50K
(ii) Equilibrium Td Estimates
- The zeroth order calculation was done in 8-b-iv above: (link)
 dust heating balances black body cooling, with
both modified by efficiency (Q) factors
dust heating balances black body cooling, with
both modified by efficiency (Q) factors
For pure black bodies, this yields the Eddington values, which are too low by factors ~few.
- To improve on this we need :
the absorption and emission efficiencies, Qabs(a, ,m) and Qem(a,
,m) and Qem(a, ,m)
,m)
which need integrating over grain size distribution, and incident and outgoing spectra
if the region is ionized, one should include the important isotropic trapped Ly field
field
any collisional heating terms should also be included
- Let's consider the most important factors: Qabs and Qem
Treating grains as black bodies: Qabs = Qem = 1 at all  is:
is:
OK in the UV - they are good absorbers
BAD in the IR - they are poor emitters (since a <<  ).
).
 the correction factor [Qabs(UV)/Qem(IR)]1/4 > 1
the correction factor [Qabs(UV)/Qem(IR)]1/4 > 1
 the resulting "green-house effect" pushes
Td above the Eddington value.
the resulting "green-house effect" pushes
Td above the Eddington value.
Fortunately, uncertainties in the correction term are muted by the 1/4 power.
- Let's use the Mie theory from above to estimate the correction term
First, consider the absorption efficiency for optical/UV starlight:
For grain sizes ~0.1µm, X = 2 a/
a/
 1 - 5 for
1 - 5 for 
 5000A - 1000A
5000A - 1000A
 Qabs ~ 1 even for poorly absorbing grains (m = 1.5 -0.05i) (see figure).
Qabs ~ 1 even for poorly absorbing grains (m = 1.5 -0.05i) (see figure).
But, at longer wavelengths and smaller grains Qabs drops well below 1
 in practice, then, L
in practice, then, L should be replaced by L
should be replaced by L ,UV and Qabs can be set to 1
,UV and Qabs can be set to 1
- For Qem(IR) we use Kirchoff's law and ask instead: what is Qabs(IR) ?
Again, relying on Mie theory; for  >> a, we have
Qabs
>> a, we have
Qabs  -4 X Im[M]
-4 X Im[M]
for a~0.1µm, X = 2 a/
a/ ~ 0.005 in the FIR
~ 0.005 in the FIR
Im[M] ~ -0.5  -0.025 for 1.5-1.0i (eg metal oxide)
-0.025 for 1.5-1.0i (eg metal oxide)  m = 1.5-0.05i (eg an ice)
m = 1.5-0.05i (eg an ice)
 Qem(FIR) = Qabs(FIR) ~ 0.01 - 0.0005.
Qem(FIR) = Qabs(FIR) ~ 0.01 - 0.0005.
- Thus, our correction factor to Td is (Qabs/Qem)1/4 ~
3 - 7
We expect ~3 for poor dielectrics/shorter wavelengths/warmer temps/larger grains
We expect ~7 for good dielectrics/longer wavelengths/colder temps/smaller grains
- Using the modified equilibrium relation, we find:
- Interstellar dust, warmed by a weak isotropic radiation field: Js ~ 0.002 erg/s/cm2/sr yields
Td ~ ( Js/
Js/ )1/4 × (Qabs/Qem)1/4
)1/4 × (Qabs/Qem)1/4  3.2 × 5 ~ 15K
3.2 × 5 ~ 15K
This cold component is called interstellar "cirrus", and emits in the FIR ~ 100-300µm
It is seen in other galaxies when not dominated by warmer (eg star formation) components
It is slightly warmer in Ellipticals, with their higher interstellar radiation field.
It probably shows a temperature gradient decreasing outwards, as Js declines.
- Because they are complex environments, HII regions have a range of Td
Close to O stars Td ~ 50K; In shrouded regions Td ~ 10K
Heating by trapped Ly is often important: Td ~ 100K
is often important: Td ~ 100K
- Deep inside DMCs, shielded from all external radiation, Td ~ few K
Here, the source of heating is X-rays from the surrounding hot phase, and cosmic rays.
- In AGN the dust can be appreciably warmer, for example:
using LAGN ~ 1010 L and grain green-house factor ~5, we get
and grain green-house factor ~5, we get
 Narrow Line Region (~100pc) temperatures: Td ~ 100K
Narrow Line Region (~100pc) temperatures: Td ~ 100K
 Broad Line Region (~0.1 pc) temperatures: Td ~ 3000K
Broad Line Region (~0.1 pc) temperatures: Td ~ 3000K
AGN's typically have "warm" IRAS colors from NLR dust: F25 / F60 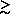 3 ×
F60 / F100
3 ×
F60 / F100
Note that dust may not survive in the BLR: Td 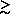 Tsublimate ~ 2000 K (check)
Tsublimate ~ 2000 K (check)
(iii) Thermal Spikes from Single Photons
- There are some puzzling observations:
sometimes, where we expect Td ~ 30K, we find 2 - 25µm emission
 Td
Td  1000K !!
1000K !!
there are galactic sources where Td is independent of distance from the central star
How do we understand these results?
- A population of very small grains:
 100 atoms; possibly PAH
100 atoms; possibly PAH
For these grains a single UV photon carries enough energy to heat the entire grain to ~ 1000K.
e.g. 1000A photon has 10eV, and a grain of N atoms has thermal capacity ~3Nk per Kelvin
 10eV = 3Nk
10eV = 3Nk T giving
T giving
 T ~ 500K for an N=100 atom grain.
T ~ 500K for an N=100 atom grain.
 well above the equilibrium temperature from a classical (non-photon) radiation field.
well above the equilibrium temperature from a classical (non-photon) radiation field.
Such hot grains radiate in the NIR
- However, they don't stay hot long !!
At a few 100K they quickly radiate their thermal energy: tcool  1 second
1 second
These grains have a "spikey" thermal history: mostly cold, with brief spikes of a few 100K
(image)



(10) Dust: Emission & Absorption
(a) Line & Band Features
- Lines & band features derive from specific bond stretching or bending modes
However, they are shifted and/or broadened due to the lattice environment.
Most, though not all, of these features are now identified.
- Examples:
- There is a very broad near-UV absorption feature centered at 2175A
it is thought to arise from a surface charge resonance on small (20nm) graphite grains.
- The 3-12µm region has several PAH features (image)
e.g. 3.3, 6.2, 7.7, 8.6, 11.3, 12.7µm
these arise from various C-H and C-C bending and stretching modes.
- Broad silicate absorption (and emission) features (see fig)
3.1µm : O-H stretch
6µm : H-O-H bend
9.7µm : Si-O stretch
18µm : Si-O-Si bend
- The so-called Diffuse Infrared Bands (DIB) are emission/absorption features near
??-??µm
their total and relative strengths vary, though are relatively low
their origin is still unknown. uncertain.
(b) Dust Absorption



(11) Dust Emission from Galaxies
- The appearance of dust in galaxies has a long History: (see Topic 1.2c)
In 1920 Curtis used dust lanes to argue (correctly) for the external nature of Spiral Nebulae,
edge on nebulae have dark lanes which resemble the Milky Way's "zone of avoidance"
 Spiral Nebulae are external versions of MW.
Spiral Nebulae are external versions of MW.
- Dust is ubiquitous: it is found in ~all galaxies; and throughout each galaxy
(e.g. Sombrero)
however, its role can vary greatly from one galaxy to the next.
- The subject has developed slowly: recent progress has been due mainly to advances in IR detection.
(a) Absorption of Galaxy Light
- since dust size a
 0.5µm it absorbes UV & optical efficiently
0.5µm it absorbes UV & optical efficiently
This can have two important impacts on our measurement of galaxies:
it affects the optical/UV appearance, hiding important regions
it can significantly reduce their apparent luminosity,
 undermines studies of, e.g.,
M/L ratios; Tully-Fisher relation; Dark Matter.
undermines studies of, e.g.,
M/L ratios; Tully-Fisher relation; Dark Matter.
Need to understand and correct for this absorption.
One approach: study how galaxy photometry depends on galaxy inclination.
(i) Inclination Effects
- This also has a long history; Holmberg (1950s) plots <µB> vs a/b (mean surface brightness vs inclination)
On average, as galaxies change from face on to edge on, one expects:
if optically thin, one expects inclined galaxies to be brighter (same light, less projected area)
if optically thick, one expects inclined galaxies to be same or dimmer (only see to AV ~ 1).
 he finds dust dimming is modest-to-important
he finds dust dimming is modest-to-important
- Since then, there have been many "correction formulae" published:
 mi = f(a/b, Hubble Type) [Topic 3.7e]
mi = f(a/b, Hubble Type) [Topic 3.7e]
Applying these corrections reduces scatter in astrophysically meaningful plots (figure)
- Be alert: some formulae correct to "face on"; others to "dust free", e.g.
RC3 corrects to face on
RSA corrects to dust free
these can differ in B by ~1 mag for the same galaxy !
(ii) Perpendicular Opacity of Disks
A critical question is whether disks are optically thick or thin.... Much debate in the 1990s.
Without rehashing that debate, it now seems that disks are:
optically thick towards the center, but transparent at the edges
thick in patches, particularly near spiral arms
there can be significant variations between galaxies.
In response to the overall uncertainties,
 most work on M/L ratios (e.g. TF relation) is now done in
the near IR (I or H band)
most work on M/L ratios (e.g. TF relation) is now done in
the near IR (I or H band)
(iii) Hidden Star Formation
Near-IR & Mid-IR imaging can reveal optically invisible star formation regions
- in normal spiral disks, obscured SF knots can be seen in spiral arms (e.g. M51)
- in starbursts, much dust is made which obscures the optical light.
 burried super star clusters emerge in the IR (e.g. the antennae)
burried super star clusters emerge in the IR (e.g. the antennae)
 from SB to LIG to ULIG; LFIR up by 103 while Lopt up by only ×3 (see Topic 11.7d and SED image)
from SB to LIG to ULIG; LFIR up by 103 while Lopt up by only ×3 (see Topic 11.7d and SED image)
- At the highest luminosity, there is a population of optically invisible z~2 ULIGs
 probably young, buried SB/QSO before blow-out.
probably young, buried SB/QSO before blow-out.
(b) Emission: Broad Band SEDs
- FIR emission from dust is a ubiquitous feature of galaxy spectra
since stars emit ~no radiation beyond 25µ, dust dominates the Mid- Far-IR
Since starbursts & AGN are powerful UV emitters, & dust is a good UV absorber:
 sometimes, Mid-Far-IR from dust dominates entire galaxy SED
sometimes, Mid-Far-IR from dust dominates entire galaxy SED
- As an example, here is the MW's ISM SED, and the SED of two AGN:
figures
(i) Four Contributions to the FIR
Mid- and Far-IR emission can have varying contributions from :
- Cold dust in the general ISM heated by the blue/UV ISRF ("cirrus")
10 - 30K  60 - 500µ
60 - 500µ
- Warmer dust in molecular clouds heated by nearby star formation
50 - 100K  25 - 100µ
25 - 100µ
- Yet warmer dust heated by an AGN
150 - 200K  adds a 25µ component
adds a 25µ component
- Hotter dust in winds from evolved red giants
100 - 1000K  12 - 25µ
12 - 25µ
(ii) Other Factors Affecting the IR output
- Current & past star formation rates
UV output is a strong function of age (highest for current massive star formation).
- Metallicity & dust composition/size distribution
composition & particle size affects absorption & radiation (e.g. single photon heating)
- Relative location of dust & sources of radiation
UV flux defines eqlm dust temperature (dust close to SF; galaxy nuclei; is warmer)
(iii) Variation Along the Hubble Sequence
- A number of properties vary systematically along the Hubble sequence, E
 Sc (see Topic 2.9)
Sc (see Topic 2.9)
e.g. star formation rates increase & HI content increases
 one might expect systematic variation of FIR/dust emission with Hubble sequence.
one might expect systematic variation of FIR/dust emission with Hubble sequence.
- Often color-color plots are useful
e.g. for IRAS with 4 bands: 12µ 25µ 60µ 100µ, one can define colors in two common ways:
- Log of flux ratio [12]/[25]
 log(F12/F25), with F12 = f
log(F12/F25), with F12 = f at 12 µ in Jansky's (i.e. per Hz)
at 12 µ in Jansky's (i.e. per Hz)
- An effective two-point spectral index, e.g.
 1225, where
1225, where  is defined by f
is defined by f



Here are two such plots for various galaxy types: (image)
- Understanding these FIR color-color plots was slow to develop
One must consider two dust types:
- large grains at eqlm temp, which increases with SFR
these affect the 25-60-100µ fluxes
- small stochastically (quantum) heated grains with ~fixed (high) temperature
these affect the 12-25µ fluxes
And three radiation fields:
- high flux UV field from young stars
- UV from older population, whose flux depends on stellar density
- an AGN, if present.
- The FIR colors arise in the following way:
- Low SFR disks (e.g. Sa) have cirrus so cold that its 25µ flux is very low:
 the large grains have low (cold) [60]/[100]
the large grains have low (cold) [60]/[100]
 the small grains have ~ equal F12 & F25
the small grains have ~ equal F12 & F25
- high SFR in irregulars (Sdm - Im) have warmer large grain emission,
 [60]/[100] is higher, and begins to dominate the F25 band
[60]/[100] is higher, and begins to dominate the F25 band
 with F25 rising fast, the [12]/[25] now appears low
with F25 rising fast, the [12]/[25] now appears low
- In ellipticals & SOs, there is little/no star formation, however:
Es & SOs have high stellar densities in the bulge with correspondingly high ISRF
dust, if it is present, is usually in the nuclear regions, where the ISRF is high.
 cirrus has intermediate temperature, with intermediate [12]/[25] & [60]/[100]
cirrus has intermediate temperature, with intermediate [12]/[25] & [60]/[100]
 FIR luminosities consistent with heating by
UV from post AGB stars (r
FIR luminosities consistent with heating by
UV from post AGB stars (r  1 kpc)
1 kpc)
(there is still some disagreememt over whether red giant winds contribute in E/SOs).
- Dust composition is also relevent:
It seems: from Im (low Z)  E (high Z), small/large grain ratio increases.
E (high Z), small/large grain ratio increases.
(iv) Starbursts
The IR SEDs of starbursts is discussed in Topic 11.7d
Briefly, as the luminosity of the starburst increases (see image)
 LIR increases correspondingly; ~×103 @ ULIGS
LIR increases correspondingly; ~×103 @ ULIGS
 however, absorption suppresses optical increase to ~×3-4
however, absorption suppresses optical increase to ~×3-4
 dust temperature gets warmer, mainly at 60µ (30-60K)
dust temperature gets warmer, mainly at 60µ (30-60K)
(v) AGN
- Accretion power in AGN generates an intense "hard" spectrum
This can heat dust in the near-nuclear regions.
 in the kpc-scale NLR, Td ~ 150-200K giving a 25µ component.
in the kpc-scale NLR, Td ~ 150-200K giving a 25µ component.
 in the sub-pc sclae BLR, Td ~ 500-1000K
in the sub-pc sclae BLR, Td ~ 500-1000K
can give a Near-IR component 1-5µ (though may not survive)
- At higher luminosity, the dust signature may depend on age:
early: post-merger, SB+AGN, shrouded
late: ISM blown away, SB declines  bare AGN dominated SED.
bare AGN dominated SED.
(c) Emission: Spectral Features
While the IR has many spectral features, there are two major features attributable to dust:
-






 a gaseous component held "down" by gravity
a gaseous component held "down" by gravity  1% Mstars
1% Mstars  5 cm of Earth's atmosphere (~1 meter of air to the GC).
5 cm of Earth's atmosphere (~1 meter of air to the GC).
 gas cycle
gas cycle  ; [CII]
; [CII] 158µ) can be major coolants
158µ) can be major coolants
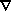
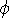

 n2
n2 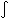 <n2> dl pc cm-6
<n2> dl pc cm-6  ~ 1%
~ 1% 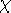 for H, He, He+ are 13.6, 24.6, 54.4 eV (= 91, 50, 25 nm)
for H, He, He+ are 13.6, 24.6, 54.4 eV (= 91, 50, 25 nm)  photo
photo  E transitions yield features at many wavelengths:
E transitions yield features at many wavelengths:
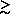 105K, H & He are fully ionized, and
kT ~ EUV - soft X-ray
105K, H & He are fully ionized, and
kT ~ EUV - soft X-ray
 it is
it is 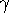
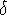
 air] !!
air] !!  ) × (
) × ( we have:
we have:  Carina).
Carina).
 phonon so collisions lose energy to lattice and adhere
phonon so collisions lose energy to lattice and adhere  75% filling factor).
75% filling factor).
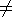 0) then Qext
0) then Qext  d
d , we have :
, we have :
 =
0.016
=
0.016