- A simple derivation of their functional forms is given here: [image]
For the radial and tangential velocities, we find:
Where Oort's constants A and B are given by (R0 = solar radius):
Oort's A expresses local shear, while
Oort's B expresses local vorticity, ie local rotation:  loc =
loc =  × V (curl V)
× V (curl V)
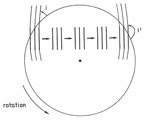
- Here are some examples of apparent stellar motions for several different rotation curves:
[image]
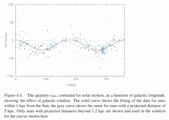
- Current best (Hipparcos) estimates for Oort's A and B are (B&M p642): [image]
A = 14.8 ± 0.8 km/s/kpc and
B = -12.4 ± 0.6 km/s/kpc
Notice their dimensions are velocity gradients which are also frequencies
E.g. using psm units: A = 0.0148 km/s/pc  0.014 Myr-1 = 14.8 Gyr-1
0.014 Myr-1 = 14.8 Gyr-1
- From their definition some interesting properties of the MW rotation can be measured:
The first of these confirms that the rotation curve is fairly flat near the sun (gently rising).
The second yields an orbital period for the sun:
P(R0) = 2 /
/  (R0) = 2
(R0) = 2 / 27.2 Gyr-1 = 0.23 Gyr = 230 Myr
/ 27.2 Gyr-1 = 0.23 Gyr = 230 Myr
And when coupled with an estimate for the galactocentric distance, R0, yields an orbital velocity:
Vc(R0) = 218 (R0 / 8 kpc) km/s
Which agrees fairly well with radio VLBI measurements of  from proper motion of Sgr A*
from proper motion of Sgr A*
Vc(R0) = 241 (R0 / 8 kpc) km/s
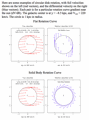
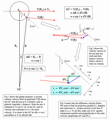
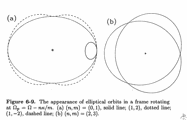
- This analysis assumes the sun and stars are all on circular orbits.
In truth, this is only approximately true: the stars are in fact perturbed from circular orbits.
This kind of motion can be analyzed using the concept of epicycles.
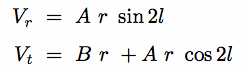
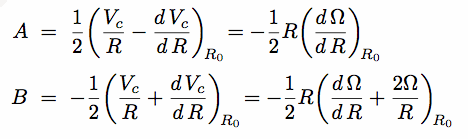
 loc =
loc = 

 0.014 Myr-1 = 14.8 Gyr-1
0.014 Myr-1 = 14.8 Gyr-1
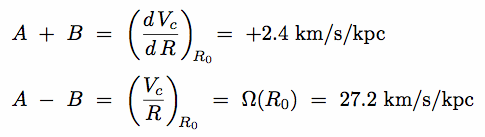
 /
/  , retrograde
, retrograde
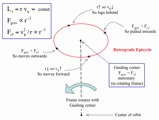
 ,
since r increases, v
,
since r increases, v w.r.t. the guiding center, the star moves backwards
w.r.t. the guiding center, the star moves backwards  v
v
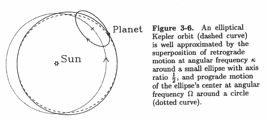
 (R,z)
(R,z) 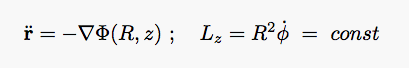

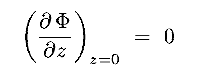
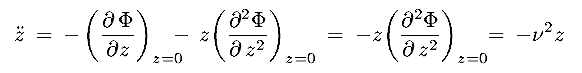
 where
where  2
2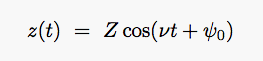
 o,
which gives
o,
which gives 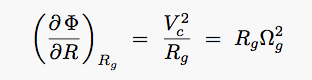
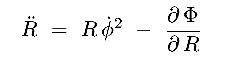
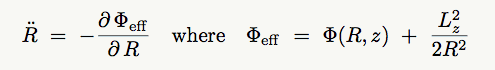
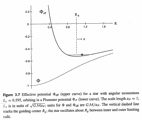
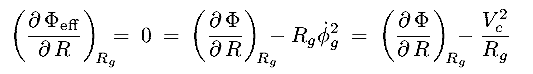
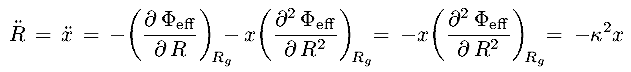
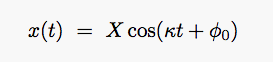
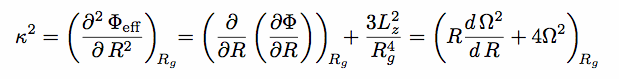
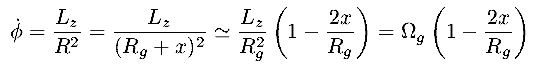
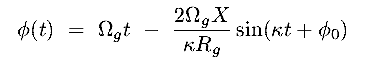
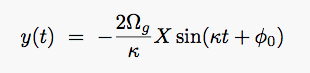
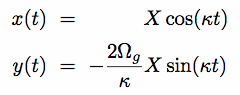
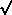 2
2

 R /
R / 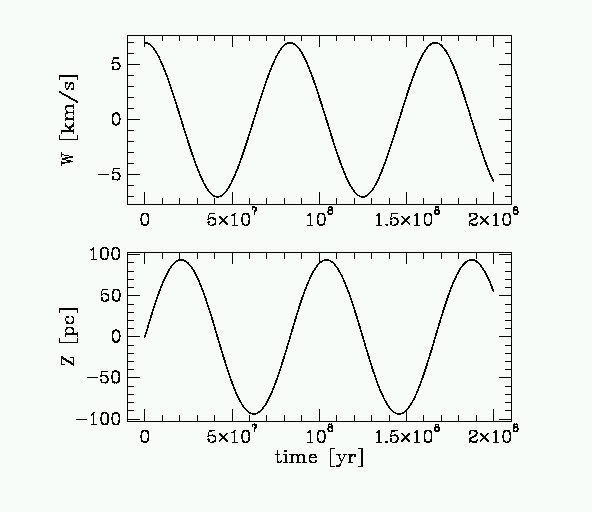
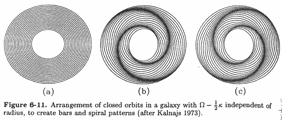
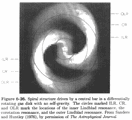
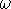 = f(k) with phase velocity,
= f(k) with phase velocity, 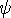 (R) ~ const, yielding logarithmic spirals
(R) ~ const, yielding logarithmic spirals 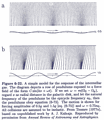



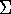 )
)
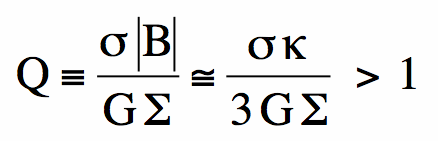
 Vs
Vs  pc-2 ;
pc-2 ;